Question

The shortest distance of $\left( 0,0 \right)$ from the curve $y=\dfrac{{{e}^{x}}+{{e}^{-x}}}{2}$ is \[\]
A.$\dfrac{1}{2}$ \[\]
B.$\dfrac{1}{3}$ \[\]
C.2 \[\]
D. None of these \[\]

Answer 1

Hint: We use distance formula between any two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ on a plane $D=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ to find the distance between origin $\left( 0,0 \right)$ and any point on the curve $\left( t,\dfrac{{{e}^{t}}+{{e}^{-t}}}{2} \right)$. We use the first derivative test to minimum distance for shortest path by finding critical points $t=c$ from $\dfrac{d}{dt}D\left( t \right)=0$ and then check if $D\left( t \right)$ changes its sign from negative to positive when we pass $t=c$. If not we use the second derivative test and check if $\dfrac{{{d}^{2}}}{d{{t}^{2}}}D\left( t \right)>0$ at $t=c$. \[\]

Complete step by step answer:
We are given in the question the equation of the following curve
\[y=\dfrac{{{e}^{x}}+{{e}^{-x}}}{2}\]
Let us take represent any point on the curve with variable $t$ as $\left( t,\dfrac{{{e}^{t}}+{{e}^{-t}}}{2} \right)$. We use the distance formula between two points and find the distance $D$ between origin $\left( 0,0 \right)$ and any point on the curve as
\[\begin{align}
  & D=\sqrt{{{\left( t-0 \right)}^{2}}+{{\left( \dfrac{{{e}^{t}}+{{e}^{-t}}}{2}-0 \right)}^{2}}} \\
 & \Rightarrow D\left( t \right)=\sqrt{{{t}^{2}}+{{\left( \dfrac{{{e}^{t}}+{{e}^{-t}}}{2} \right)}^{2}}} \\
\end{align}\]
We expand ${{\left( {{e}^{t}}+{{e}^{-t}} \right)}^{2}}$ using the algebraic identity ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab$for $a={{e}^{t}},b={{e}^{-t}}$ to have the distance function as;
\[\begin{align}
  & \Rightarrow D\left( t \right)=\sqrt{{{t}^{2}}+\dfrac{{{\left( {{e}^{t}} \right)}^{2}}+{{\left( {{e}^{-t}} \right)}^{2}}+2{{e}^{t}}{{e}^{-t}}}{{{2}^{2}}}} \\
 & \Rightarrow D\left( t \right)=\sqrt{{{t}^{2}}+\dfrac{{{e}^{2t}}+{{e}^{-2t}}+2}{4}} \\
\end{align}\]

The shortest distance between the origin and any point on the curve will occur when the distance function $D\left( t \right)$ is minimum. So let us use first derivative test to find the minima. So we first find the critical points by equating the first derivative of the function to zero. We differentiate $D\left( t \right)$ with respect to $t$ and have;
\[\dfrac{d}{dt}D\left( t \right)=\dfrac{d}{dt}\left( \sqrt{{{t}^{2}}+\dfrac{{{e}^{2t}}+{{e}^{-2t}}+2}{4}} \right)\]
We use the chain rule for differentiation to have;

\[\begin{align}
  & \Rightarrow \dfrac{d}{dt}D\left( t \right)=\dfrac{1}{2\sqrt{{{t}^{2}}+\dfrac{{{e}^{2t}}+{{e}^{-2t}}+2}{4}}}\left( \dfrac{d}{dt}\left( {{t}^{2}}+\dfrac{{{e}^{2t}}+{{e}^{-2t}}+2}{4} \right) \right) \\
 & \Rightarrow \dfrac{d}{dt}D\left( t \right)=\dfrac{1}{2D\left( t \right)}\left( \dfrac{d}{dt}{{t}^{2}}+\dfrac{d}{dt}\left( \dfrac{{{e}^{2t}}}{4} \right)+\dfrac{d}{dt}\left( \dfrac{{{e}^{-2t}}}{4} \right)+\dfrac{d}{dt}\left( \dfrac{2}{4} \right) \right) \\
 & \Rightarrow \dfrac{d}{dt}D\left( t \right)=\dfrac{1}{2D\left( t \right)}\left( 2t+\dfrac{1}{2}{{e}^{2t}}-\dfrac{1}{2}{{e}^{-2t}} \right).....\left( 1 \right) \\
\end{align}\]
We equate the obtained derivative to zero to find the critical points;
\[\begin{align}
  & \dfrac{1}{2D\left( t \right)}\left( 2t+\dfrac{1}{2}{{e}^{2t}}-\dfrac{1}{2}{{e}^{-2t}} \right)=0 \\
 & \Rightarrow 2t+\dfrac{1}{2}{{e}^{2t}}-\dfrac{1}{2}{{e}^{-2t}}=0 \\
 & \Rightarrow 4t+{{e}^{2t}}-{{e}^{-2t}}=0 \\
\end{align}\]
We can use trial and error method and find the only root of the above equation as $t=0$.So $t=0$ is a critical point at and since distance function cannot be negative and will not sign change at $t=0$.We have to use the double derivative test. So let us differentiate $\dfrac{d}{dt}D\left( t \right)$ with respect to $t$ once again in (1) to have;

\[\begin{align}
  & \dfrac{d}{dt}\left( \dfrac{d}{dt}D\left( t \right) \right)=\dfrac{1}{2D\left( t \right)}\left( 2t+\dfrac{1}{2}{{e}^{2t}}-\dfrac{1}{2}{{e}^{-2t}} \right) \\
 & \Rightarrow \dfrac{{{d}^{2}}D\left( t \right)}{d{{t}^{2}}}=\dfrac{1}{2}\left[ \dfrac{-1}{{{D}^{2}}\left( t \right)}\left( 2t+\dfrac{1}{2}{{e}^{2t}}-\dfrac{1}{2}{{e}^{-2t}} \right)+\dfrac{1}{D\left( t \right)}\left( t+{{e}^{t}}+{{e}^{-t}} \right) \right] \\
\end{align}\]
We put $t=0$ in the above step to have;
\[\begin{align}
  & \Rightarrow {{\left. \dfrac{{{d}^{2}}D\left( t \right)}{d{{t}^{2}}} \right|}_{t=0}}=\dfrac{1}{2}\left[ \dfrac{-1}{{{D}^{2}}\left( 0 \right)}\left( 2\times 0+\dfrac{1}{2}{{e}^{2\times 0}}-\dfrac{1}{2}{{e}^{-2\times 0}} \right)+\dfrac{1}{D\left( t \right)}\left( 0+{{e}^{0}}+{{e}^{-0}} \right) \right] \\
 & \Rightarrow {{\left. \dfrac{{{d}^{2}}D\left( t \right)}{d{{t}^{2}}} \right|}_{t=0}}=\dfrac{1}{2}\left[ 0+\dfrac{1}{D\left( t \right)}\left( 1 \right) \right] \\
 & \Rightarrow {{\left. \dfrac{{{d}^{2}}D\left( t \right)}{d{{t}^{2}}} \right|}_{t=0}}=\dfrac{1}{2D\left( t \right)}\ge 0\left( \because \text{ since distance is always postive } \right) \\
\end{align}\]


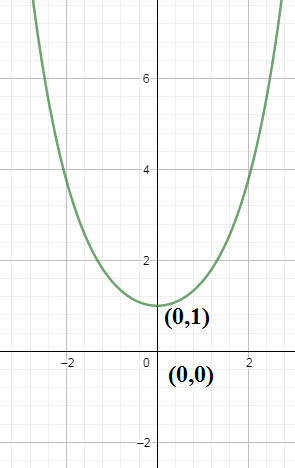
So there is a minima occurs at $t=0$ for $D\left( t \right)$ and the point minima is $\left( t,\dfrac{{{e}^{t}}+{{e}^{-t}}}{2} \right)=\left( 0,\dfrac{{{e}^{0}}+{{e}^{-0}}}{2} \right)=\left( 0,1 \right)$. So the shortest path of the curve from the origin is the distance between $\left( 0,1 \right)$ and $\left( 0,0 \right)$ which we can find using the distance formula as 1.

So, the correct answer is “Option D”.

Note: We note that the given function $\dfrac{{{e}^{x}}+{{e}^{-x}}}{2}$ is the cosine hyperbolic $\cosh x$ function whose curve we have plotted and whose differentiation is the sine hyperbolic function $\sinh x=\dfrac{{{e}^{x}}-{{e}^{-x}}}{2}$. If we find the minimization of $D\left( t \right)$ difficult we can also minimize ${{D}^{2}}\left( t \right)$ instead. We should remember that the critical points not only occur at ${{f}^{'}}\left( x \right)=0$ but also at the points the derivative is not defined.