Question

The shortest distance between two tetrahedral voids is:
(A) $ \text{a}\sqrt{\text{3}} $
(B) $ \dfrac{\text{a}\sqrt{\text{3}}}{2} $
(C) $ \dfrac{\text{a}}{2} $
(D) $ \dfrac{\text{a}\sqrt{\text{3}}}{4} $

Answer 1

Hint: The voids in the crystals can be defined as the region of empty space between the molecules of the crystals and this empty space is the region which lies outside the normal van der Waals surface area of molecules in the unit cells and within which no nuclei of the atoms exists.

Complete step by step solution:
To answer this question, let us take the example of the Face Centred Cubic Crystal system. There are a total 8 tetrahedral voids in a Face Centred Cubic lattice. Now if we divide the Face Centred Cubic lattice into 8 smaller cubes then each cube will have one tetrahedral void at the centre of the cube at the body centre of the small cubes. Now if we consider the length of the side of the big Face Centred Cube be a, then on breaking into smaller cubes the edge length of each cube will be $ \dfrac{\text{a}}{2} $ .
The figure below will reveal the situation better:

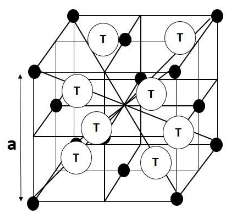
From the figure it is clear that the distance between two tetrahedral voids in a cube is equal to $ \dfrac{\text{a}}{2} $ .
The correct answer here is option C.

Note:
There are two types of voids in the crystal structures: the tetrahedral voids and the octahedral voids. The tetrahedral voids are empty spaces between the particles in a unit cell of a tetrahedral crystal structure, whereas the octahedral voids are the empty spaces between the particles that are present in the unit cell of an octahedral crystal system.