Question

The shortest distance between two intersecting lines is always equal to _________.

Answer 1

Hint: The shortest distance between two lines is equal to determining how far apart lines are. This can be done by measuring the length of a line that is perpendicular to both of them. and in this case, we have two intersecting lines.

Complete step-by-step answer:
                                               

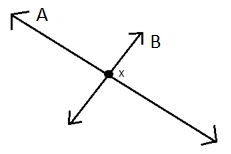
In this figure, we have two straight lines A and B. which intersect each other at point x as shown in figure. (Intersecting lines are the ones which intersect each other at one point.)
Now, as we know we need to calculate the shortest distance between two intersecting lines. And in this we say line A and B.
Since the lines are bound to intersect at one point,
The shortest distance between them would always be equal to 0.
Therefore, The shortest distance between two intersecting lines is always equal to 0.


Note- We may use formulas directly to find the shortest distance between two parallel lines. For two non-intersecting lines lying in the same plane, the shortest distance is the distance that is shortest of all the distances between two points lying on both lines.
If the equations of two parallel lines are expressed in the following way:
ax + by + ${{\text{d}}_{\text{1}}}$ = 0 and ax + by + ${{\text{d}}_{\text{2}}}$ = 0
Then, the formula for shortest distance can be written as under:
   ${\text{d = }}\dfrac{{|{d_2} - {d_1}|}}{{\sqrt {{a^2} + {b^2}} }}$ .