Question

The shape of the top surface of a table is trapezium. Find the area if its parallel sides are \[1m\] and $1.2m$ and perpendicular distance between them is $0.8m$.

Answer 1

Hint: Trapezium is a quadrilateral with one pair of opposite sides parallel. We can find the area of a trapezium if the lengths of the parallel sides and the perpendicular distance between them are known. Substituting those in the formula we get the answer.

Useful formula:
Area of a trapezium, $A = \dfrac{1}{2}h(a + b)$ where $a$ and $b$ are the parallel sides and $h$ is the perpendicular distance between them.

Complete step-by-step answer:
It is said that the shape of the top surface of a table is trapezium.
Also we have, its parallel sides are \[1m\] and $1.2m$ and perpendicular distance between them is $0.8m$.

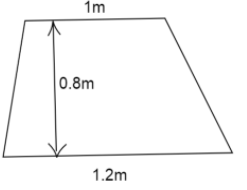
We are asked to find its area.
Area of a trapezium, $A = \dfrac{1}{2}h(a + b)$ where $a$ and $b$ are the parallel sides and $h$ is the perpendicular distance between them.
Substituting these values we get,
The area of the top surface, $A = {\text{Area of the trapezium}}$
$ \Rightarrow A = \dfrac{1}{2} \times 0.8 \times (1 + 1.2)$
Simplifying we get,
$ \Rightarrow A = \dfrac{1}{2} \times 0.8 \times 2.2$
For ease of calculation we can write $0.8$ as $\dfrac{8}{{10}}$ and $2.2$ as $\dfrac{{22}}{{10}}$.
This gives,
$ \Rightarrow A = \dfrac{1}{2} \times \dfrac{8}{{10}} \times \dfrac{{22}}{{10}}$
Since $8 = 2 \times 4$ , we can write
$ \Rightarrow A = \dfrac{{4 \times 22}}{{100}}$
$ \Rightarrow A = \dfrac{{88}}{{100}} = 0.88$
This gives the area of the top surface of the table as $0.88{m^2}$.

Additional information:
If the non-parallel sides of the trapezium are equal, those ones are specially called as isosceles trapezium.

Note: Here we are given three measurements of the trapezium. These are mandatorily known to find the area. We could not find the area if we were given the lengths of the non-parallel sides instead