Question

The shape of $C{{H}_{4}}$, $SO_{4}^{2-}$, $PO_{4}^{3-}$ is-
a) Trigonal
b) Angular
c) Tetrahedral
d) Trigonal bipyramidal

Answer 1

Hint: We can know the shape of these molecules with the help of hybridization. Hybridization is the intermixing of orbitals to form new orbitals of equivalent energy and by using the formula as $H=\dfrac{1}{2}(v+m-c+a)$, we can find the hybridization and know the shapes of these molecules. Now solve it.

Complete answer:
First of all, let’s discuss what hybridization is. By the term hybridization, we simply mean the intermixing of the orbitals of slightly different energies so as to redistribute their energies and to give a new set of orbitals of equivalent energies and shape. It is denoted by H.
It is not necessary in hybridization that only half-filled orbitals participate in it . In certain cases, even the filled orbitals of the valence shell participate in hybridization.
We can calculate the hybrids ion by using the formula as;-
$H=\dfrac{1}{2}(v+m-c+a)$
Here, V is the electrons in the valence shell, m stands for monovalent, c is the cation and a is the anion.
Now considering the statement as;-
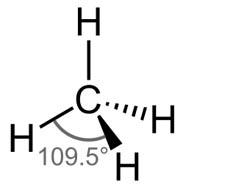
a) $C{{H}_{4}}$
$\begin{align}
  & H=\dfrac{1}{2}(4+4) \\
 & \text{ =}\dfrac{8}{2} \\
 & \text{ =4} \\
\end{align}$
So, its geometry i.e. shape is tetrahedral.

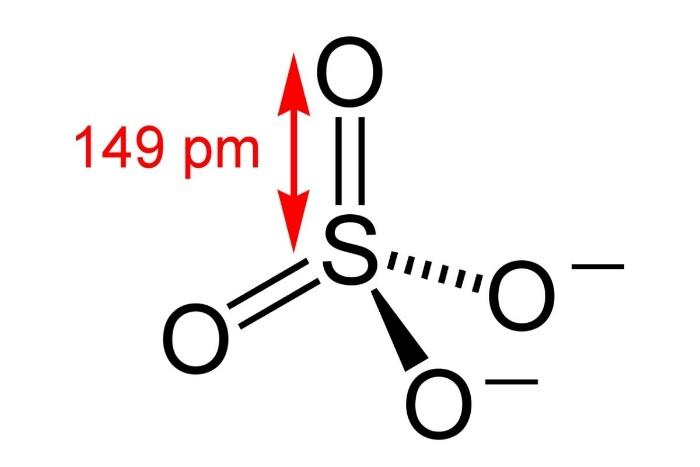
b) $SO_{4}^{2-}$
$\begin{align}
  & H=\dfrac{1}{2}(6+2) \\
 & \text{ =}\dfrac{8}{2} \\
 & \text{ =4} \\
\end{align}$
So, its geometry i.e. shape is tetrahedral.

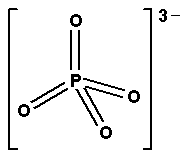
c) $PO_{4}^{3-}$
$\begin{align}
  & H=\dfrac{1}{2}(5+3) \\
 & \text{ =}\dfrac{8}{2} \\
 & \text{ =4} \\
\end{align}$
So, its geometry i.e. shape is tetrahedral.

Thus, The shape of $C{{H}_{4}}$, $SO_{4}^{2-}$,$PO_{4}^{3-}$is tetrahedral.
So, the correct answer is “Option c”.

Note:
In hybridization, the number of hybrid orbitals formed is equal to the number of orbitals that get hybridized. The hybrid orbitals are always equivalent in energy and shape and are more effective in forming stable bonds than the pure atomic orbitals.