Question

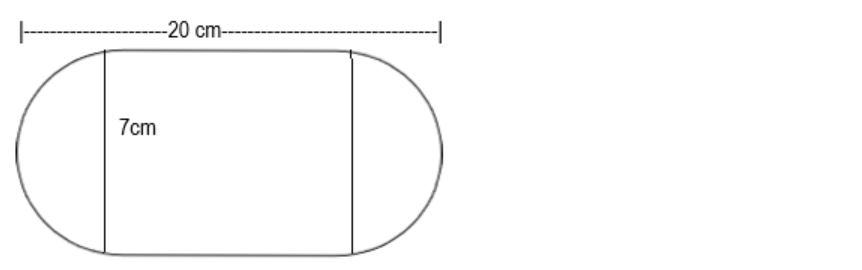
The shape of a garden is rectangular in the middle and semi-circular at the ends as shown in the diagram. Find the area and the perimeter of the garden. [Length of rectangle is \[20 - (3.5 + 3.5)\]metres]

Answer 1

Hint: We will firstly find the length and the breadth of the rectangle. With the help of these values, we will have to find the areas of the rectangle and the semi-circle separately and add them. Finally, we are going to calculate the circumference of the semi-circles to find the perimeter of the garden.

Complete step by step Answer :

Looking at the question, we know that we are given the breadth of the garden and the length of the garden.
The breadth of the rectangle is equal to the diameter of the semicircle as they share the boundaries.
So, the breadth of the rectangle=the diameter of the semi-circle\[ = 7m\]
Hence, the radius of the semicircle\[ = \dfrac{7}{2} = 3.5m\]
The length of the rectangular part of the garden\[ = 20 - (3.5 + 3.5) = 20 - 7 = 13m\]
Area of the rectangular part of the garden\[ = l \times b = 13m \times 7m = 91{m^2}\]
We know that if we combine two semi-circles, we get a full circle.
So, the area of the circle with radius \[3.5m\]
\[
   = \pi {r^2} = \dfrac{{22}}{7} \times {(3.5)^2} \\
   = \dfrac{{22}}{7} \times 3.5 \times 3.5 \\
   = 22 \times 3.5 \times 0.5 \\
   = 38.5{m^2} \\
\]
Perimeter of the circular part\[ = 2\pi r = 2 \times \dfrac{{22}}{7} \times 3.5 = 2 \times 22 \times 0.5 = 22m\]
Therefore, the perimeter of the garden
=the sum of the perimeter of both the semicircles and the length of the rectangle on both sides
=the sum of the perimeter of the circle and the length of the rectangle on both sides
\[
   = 22 + 13 \times 2 \\
   = 22 + 26 \\
   = 48m \\
\]
The area of the garden= the sum of the area of the rectangle and the area of the semicircles
= the sum of the area of the rectangle and the area of the circle
\[
   = 38.5 + 91 \\
   = 129.5{m^2} \\
\]

Therefore, the area and the perimeter of the garden is \[129.5{m^2}\& 48m\] respectively.

Note: We will have to remember all the mensuration formulas for all the figures. We might make the mistake of adding the perimeter of the rectangle with the perimeter of the circle but we have to remember that we are asked to find the perimeter or the boundary of the garden which does not include the breadth of the rectangle or the diameter of the semicircles.