Question

The shadow of the tower is 30 metres when the sun’s altitude is ${30^ \circ }$ . When the sun’s altitude is ${60^ \circ }$then the length of the shadow will be
a.60 m
b.15 m
c.10 m
d.5 m

Answer 1

Hint: Considering the sun above the tower we get the shadow of the tower to be OP when the sun's altitude is ${30^ \circ }$ and the length of the shadow to be OQ when the sun's altitude is ${60^ \circ }$and then using the tangent ratio in triangle OPS we get the value of OS and once again using the tangent ratio in triangle OQS we get the value of OQ.

Complete step-by-step answer:
Lets assume that the sun is right above the tower
Let P be the point when the altitude of the sun is ${30^ \circ }$
As the shadow of the tower is 30 m we have OP to be 30 m
Now let Q be the point when the sun's altitude is ${60^ \circ }$
And the shadow at that point of time is OQ

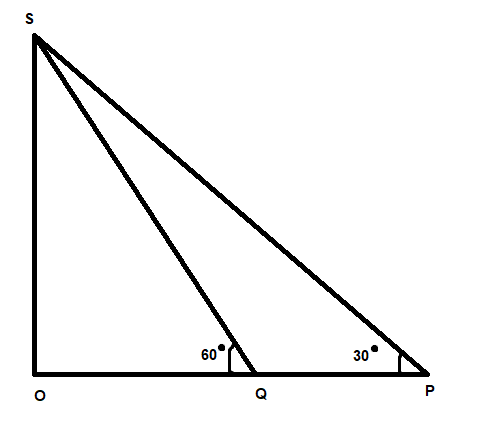
Now using the tangent ratio in the triangle OPS we get
$
   \Rightarrow \tan 30 = \dfrac{{OS}}{{OP}} \\
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{OS}}{{30}} \\
   \Rightarrow OS = \dfrac{{30}}{{\sqrt 3 }}m \\
$
Now using the tangent ratio in the triangle OQS we get
$
   \Rightarrow \tan 60 = \dfrac{{OS}}{{OQ}} \\
   \Rightarrow \sqrt 3 = \dfrac{{\dfrac{{30}}{{\sqrt 3 }}}}{{OQ}} = \dfrac{{30}}{{\sqrt 3 OQ}} \\
   \Rightarrow \sqrt 3 *\sqrt 3 OQ = 30 \\
   \Rightarrow 3OQ = 30 \\
   \Rightarrow OQ = \dfrac{{30}}{3} = 10m \\
$
Therefore the length of the shadow when the sun’s altitude is ${60^ \circ }$is 10 m
The correct option is c

Note: In problems of these kind you can be provided with any two of the following information:
(i)The distance of the object from the observer
(ii)The height of the object
(iii)Angle at which the observer views the topmost point of the object (angle of elevation)
(iv)The angle at which the observer views the object when the observer is on top of a tower/building (angle of depression)