Question

The shadow of the tower becomes 60 metres long when the altitude of the sun changes from $45{}^\circ $ to $30{}^\circ $. Then the height of the tower is
A. $20\left( \sqrt{3}+1 \right)m$
B. $24\left( \sqrt{3}+1 \right)m$
C. $30\left( \sqrt{3}+1 \right)m$
D. $30\left( \sqrt{3}-1 \right)m$

Answer 1

Hint: In order to solve this question, we should know about the concept of trigonometric ratios. Like $\tan \theta =\dfrac{Perpendicular}{Base}$ and so on. We should also know that $\tan 45{}^\circ =1,\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$. We should first draw the figure according to conditions given in the question to find our answer.

Complete step-by-step answer:
In this question, we have been asked to find the height of a tower, whose shadow length becomes 60 m longer when the altitude of sun changes from $45{}^\circ $ to $30{}^\circ $. To solve this question, we will first visualise the given situation and draw the figure accordingly. The figure is as given below.

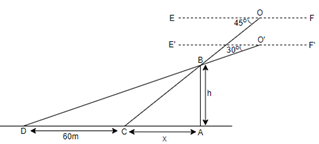
Here, we have represented the tower as AB of assumed height h and assumed AC as the shadow of the tower form position of sun as O at an altitude of $45{}^\circ $ and we have represented AD as the shadow of the tower from position of sun as O’ at an altitude of $30{}^\circ $. Now, we know that the trigonometric ratio, $\tan \theta =\dfrac{Perpendicular}{Base}$. So, in $\Delta ABC$, we can say that $\tan \angle ACB=\dfrac{AB}{AC}$ and we can write it further as,
$\tan \angle ACB=\dfrac{h}{x}\ldots \ldots \ldots \left( i \right)$
Now, we know that the altitude of the sun is measured with respect to the horizontal line. So, we can say EF, E’F’ and AD are the three parallel lines. Now, we know that parallel lines show the property of interior opposite angles. So, we can say, $\angle EOC=\angle OCA=45{}^\circ $and $\angle E'O'D=\angle O'DA=30{}^\circ $. So, we can write equation (i) as,
 $\tan 45{}^\circ =\dfrac{h}{x}$
Now, we know that $\tan 45{}^\circ =1$. Therefore, we can say,
$\begin{align}
  & 1=\dfrac{h}{x} \\
 & \Rightarrow x=h\ldots \ldots \ldots \left( ii \right) \\
\end{align}$
Also, in $\Delta ABD$, we can say that $\tan \angle BDA=\dfrac{AB}{AD}$. So, we can write this equation as,
$\tan 30{}^\circ =\dfrac{h}{x+60}$
We know that $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$, so we can say,
$\dfrac{1}{\sqrt{3}}=\dfrac{h}{x+60}$
We will put the value of x form equation (ii) in the above equation. So, we will get,
$\begin{align}
  & \dfrac{1}{\sqrt{3}}=\dfrac{h}{h+60} \\
 & \Rightarrow h+60=\sqrt{3}h \\
 & \Rightarrow 60=\sqrt{3}h-h \\
 & \Rightarrow 60=\left( \sqrt{3}-1 \right)h \\
 & \Rightarrow h=\dfrac{60}{\left( \sqrt{3}-1 \right)} \\
\end{align}$
Now, we will rationalise the denominator $\sqrt{3}-1$ by multiplying the numerator and denominator by $\sqrt{3}+1$. So, we get,
$\begin{align}
  & h=\dfrac{60}{\sqrt{3}-1}\times \dfrac{\sqrt{3}+1}{\sqrt{3}+1} \\
 & \Rightarrow h=\dfrac{60\left( \sqrt{3}+1 \right)}{3-1} \\
 & \Rightarrow h=\dfrac{60\left( \sqrt{3}+1 \right)}{2} \\
 & \Rightarrow h=30\left( \sqrt{3}+1 \right)m \\
\end{align}$
Hence, we can say that the height of the tower is $30\left( \sqrt{3}+1 \right)m$. Therefore, the correct option is option C.

Note: While solving this question, the possible mistakes is that we can choose the incorrect option as option C and D are almost similar, with just the difference of a sign. And we should remember the standard values of the trigonometric angles and not write $\tan 30{}^\circ =\sqrt{3}$ instead of $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$.