Question

The shadow of a tower, when the angle of elevation of the sun is ${45^0}$, is found to be 10 meters longer than when the angle of elevation is ${60^0}$. Find the height of the tower.
$
  (a){\text{ 15 + 5}}\sqrt 3 \\
  (b){\text{ 12 + 5}}\sqrt 3 \\
  (c){\text{ 15 + }}\sqrt 3 \\
  (d){\text{ 12 + }}\sqrt 3 \\
$

Answer 1

Hint – In this question let the height of the tower be h meters. Now when angle of elevation is 60 degree then let BC be the shadow (see diagram) equal to x, and when angle of elevation changes to 45 degree now the shadow BD is x+10 meters. Use trigonometric ratios in respective triangles to formulate two equations involving two variables. Solve them to get the answer.

Complete step-by-step solution-

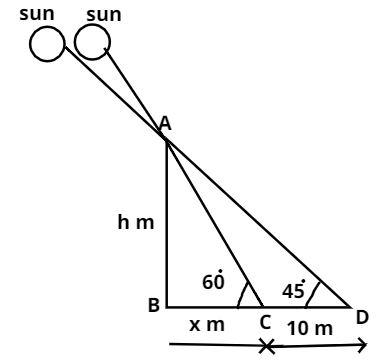
Let AB be the tower and let that the height of the tower be (h) meter.
Now let BC be the shadow of a tower when the angle of elevation of sun is 60 degree as shown in figure.
Now it is given that the shadow of the tower is increased by 10 m when the elevation of sun changes from 60 to 45 degree as shown in figure.
Therefore CD = 10 m.
Therefore from figure BD = x + 10 meter.
Now in triangle ABC tan is the ratio of perpendicular to base.
$ \Rightarrow \tan {60^0} = \dfrac{{AB}}{{BC}} = \dfrac{h}{x} = \sqrt 3 $, $\left[ {\because \tan {{60}^0} = \sqrt 3 } \right]$
$ \Rightarrow x = \dfrac{h}{{\sqrt 3 }}$ meter.................... (1)
Now in triangle ABD we have,
$ \Rightarrow \tan {45^0} = \dfrac{{AB}}{{BD}} = \dfrac{h}{{x + 10}} = 1$, $\left[ {\because \tan {{45}^0} = 1} \right]$
$ \Rightarrow h = x + 10$
Now from equation (1) we have,
$ \Rightarrow h = \dfrac{h}{{\sqrt 3 }} + 10$
Now simplify the above equation we have,
$
   \Rightarrow h - \dfrac{h}{{\sqrt 3 }} = 10 \\
   \Rightarrow h\left( {\sqrt 3 - 1} \right) = 10\sqrt 3 \\
   \Rightarrow h = \dfrac{{10\sqrt 3 }}{{\sqrt 3 - 1}} \\
$
Now multiply and divide by $\sqrt 3 + 1$ we have,
$ \Rightarrow h = \dfrac{{10\sqrt 3 }}{{\sqrt 3 - 1}} \times \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}} = \dfrac{{30 + 10\sqrt 3 }}{{3 - 1}} = \dfrac{{30 + 10\sqrt 3 }}{2} = 15 + 5\sqrt 3 $ meter.
So this is the required height of the tower.
Hence option (A) is correct.

Note – It is always advised to form the diagrammatic representation of the information provided, as it helps understanding the geometry and to keep a track which triangle needs to be taken into consideration while applying the concept of trigonometric ratio. $\operatorname{Tan} \theta $ is the most frequently used trigonometric ratio in such types of problems, so always think of this way only while attempting this type of problems.