Question

The shadow of a tower standing on the level ground to be 40m shorter when the sun's altitude changes from ${{30}^{\circ }}$ to ${{60}^{\circ }}$, find the height of tower. \[\]

Answer 1

Hint: We denote AB as the tower, C as the position of the top of the shadow of the tower AB when the sun’s altitude was ${{30}^{\circ }}$ and D as the position of the top of the shadow of the tower AB when the sun’s altitude was ${{60}^{\circ }}$. We take the tangent of the angle in the right angled triangle ABD to express BD in terms of AB. We again take tangent of the angle in the right angled triangle ABC to find another expression of BD in terms of AB. We equate the right side of both the expression to find the height of the tower AB. \[\]

Complete step-by-step answer:
We know that solar altitude is the angle of the sun rays relative to the earth's horizon, and is measured in degrees. Let A be the top and B be the bottom of the tower. Let C be the position of the top of the shadow of the tower AB when the sun’s altitude was ${{30}^{\circ }}$ and D be the position of the top of the shadow of the tower AB when the sun’s altitude was ${{60}^{\circ }}$. So we have
\[\angle ADB={{60}^{\circ }},\angle ACB=30{}^{\circ }\]
The tower is always vertical to the ground so we have
\[\angle ADB={{60}^{\circ }},\angle ABC=30{}^{\circ }\]
We are given the question that when the top of the shadow moved from C to D length of the shadow decreased by 40m which means$CD=40m$. So we have rough figure as
 

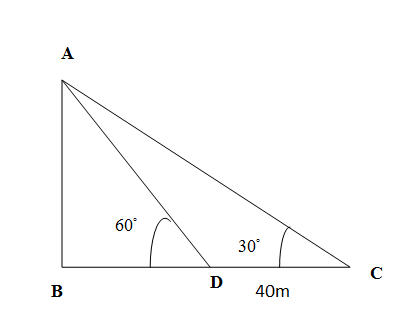
The tangent of any acute angle in the right angled triangle is the ratio of opposite side to the adjacent side (excluding hypotenuse) . We observe the right triangle ABD. We take tangent of the angle $\angle ADB$ and have,
\[\begin{align}
  & \tan \left( \angle ADB \right)=\dfrac{AB}{BD} \\
 & \Rightarrow \tan {{60}^{\circ }}=\dfrac{AB}{BD} \\
 & \Rightarrow BD=\dfrac{AB}{\tan {{60}^{\circ }}}=\dfrac{AB}{\sqrt{3}}..........\left( 1 \right) \\
\end{align}\]
We observe the right triangle ABC. We take tangent of the angle $\angle ACB$ and have,

\[\begin{align}
  & \tan \left( \angle ADB \right)=\dfrac{AB}{BC} \\
 & \Rightarrow \tan {{30}^{\circ }}=\dfrac{AB}{BD+CD} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{AB}{BD+40} \\
 & \Rightarrow BD=\sqrt{3}AB-40.....\left( 2 \right) \\
\end{align}\]
We equate the right hand sides of equation (1) and (2) as the left hand sides are equal to have,
\[\begin{align}
  & \dfrac{AB}{\sqrt{3}}=\sqrt{3}AB-40 \\
 & \Rightarrow AB=3AB-40\sqrt{3} \\
 & \Rightarrow 2AB=40\sqrt{3} \\
 & \Rightarrow AB=20\sqrt{3} \\
\end{align}\]
So the height of the tower is $AB=20\sqrt{3}$m. \[\]

Note: We can take cosines of the angle to find the length of the shadow at two different altitudes BD and BC. The altitude is zero at sunrise and sunset, and can reach a maximum of 90 degrees at noon. The altitude is also the angle of elevation of the top of any object (here tower) as from the ground. Solar zenith angle is angle subtended by sun rays with any vertical line.