Question

The shadow of a tower standing on level ground is found to be 40 m longer when the sun’s altitude is ${{30}^{\circ }}$ than when it was ${{60}^{\circ }}$. Find the height of the tower. (Given $\sqrt{3}=1.732$)

Answer 1

Hint: We have to first make the figure of the given conditions. We take the altitude and the shadow in the form of a right-angled triangle. We use the trigonometric identity of $\cot \theta $ to form the length of the shadow in the form of the height of the tower. We have the difference between the two shadows and form the equation. We solve it to find the height of the tower.

Complete step-by-step solution
First, we try to form the image from the given conditions. Given that the shadow of a tower standing on level ground is found to be 40 m longer when the sun’s altitude is ${{30}^{\circ }}$ than when it was ${{60}^{\circ }}$.

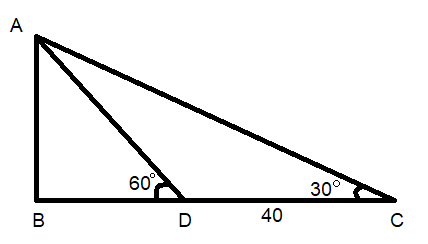
Let’s assume AB is the tower standing on level ground with height x m. So, $AB=x$.
The sun is on the left side of the tower and is casting a shadow on the right side.
When the sun’s altitude is ${{60}^{\circ }}$, it casts a shadow in the form of BD and when the sun’s altitude is ${{30}^{\circ }}$, it casts a shadow in the form of BC. The difference is 40m.
So, $\angle BDA={{60}^{\circ }},\angle BCA={{30}^{\circ }},BC-BD=40$.
We want to form the last equation in the form of the height of AB which is x.
The tower is vertical on the ground. So, $\angle ABC={{90}^{\circ }}$.
We now use trigonometric identities to find the values of BD and BC with respect to AB.
In $\Delta ABD$, $\cot \angle BDA=\dfrac{BD}{AB}$. Putting the values, we get value of BD as
$\begin{align}
  & \cot \angle BDA=\dfrac{BD}{AB} \\
 & \Rightarrow \dfrac{BD}{x}=\cot {{60}^{\circ }}=\dfrac{1}{\sqrt{3}} \\
 & \Rightarrow BD=\dfrac{x}{\sqrt{3}} \\
\end{align}$.
Now in $\Delta ABC$, $\cot \angle BCA=\dfrac{BC}{AB}$. Putting the values, we get value of BC as
$\begin{align}
  & \cot \angle BCA=\dfrac{BC}{AB} \\
 & \Rightarrow \dfrac{BC}{x}=\cot {{30}^{\circ }}=\sqrt{3} \\
 & \Rightarrow BC=\sqrt{3}x \\
\end{align}$.
We have the equation $BC-BD=40$. We put the values.
$\begin{align}
  & BC-BD=40 \\
 & \Rightarrow \sqrt{3}x-\dfrac{x}{\sqrt{3}}=40 \\
 & \Rightarrow \dfrac{2x}{\sqrt{3}}=40 \\
 & \Rightarrow x=\dfrac{40\times \sqrt{3}}{2}=20\sqrt{3} \\
 & \Rightarrow x=20\times 1.732=34.64 \\
\end{align}$.
Therefore, the length of the tower is 34.64m.

Note: We need to keep in mind that the only way it can be expressed in the form of identity when the triangles are right-angle triangles. The sides were taken with respect to the angle. We have taken the base and the height of the angle. The hypotenuse part always remains intact.