Question

The shadow of a flagstaff is three times as long as the shadow of the flagstaff when the sun rays meet the ground at an angle of ${60^0}$. Find the angle between the sun rays and ground at the time of the longer shadow.

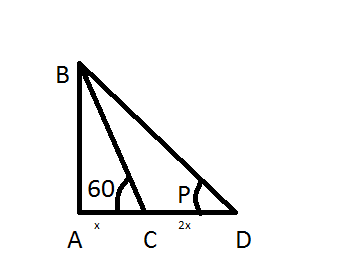
A. ${\text{P}} = {30^0}$
B. ${\text{P}} = {60^0}$
C. ${\text{P}} = {45^0}$
D. ${\text{P}} = {15^0}$

Answer 1

Hint – In order to solve this problem we need to take two triangles and use the concept of trigonometric angles and get the equations to get the angle P using the trigonometric angles itself.

Complete step-by-step answer:

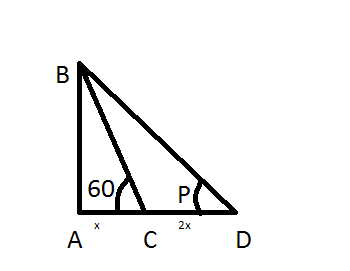
From the given figure AC = x, CD = 2x. Let AB = h and we can clearly see
AD = AC + CD = x + 2x = 3x…………….(1)
In triangle ABC we can say that,
\[
   \Rightarrow {\text{tan60 = }}\dfrac{{{\text{AB}}}}{{{\text{AC}}}} \\
   \Rightarrow \sqrt {\text{3}} {\text{ = }}\dfrac{{\text{h}}}{{\text{x}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,({\text{From}}\,(1)) \\
   \Rightarrow {\text{h = x}}\sqrt {\text{3}} .......................(2) \\
\]

In triangle ABD we can say that,
$
   \Rightarrow \tan {\text{P = }}\dfrac{{{\text{AB}}}}{{{\text{AD}}}} \\
   \Rightarrow \tan {\text{P = }}\dfrac{{\text{h}}}{{{\text{3x}}}} \\
   \Rightarrow \tan {\text{P = }}\dfrac{{{\text{x}}\sqrt {\text{3}} }}{{{\text{3x}}}} = \dfrac{1}{{\sqrt 3 }}..................({\text{From (2)}}) \\
$
So, angle P = 30 degrees.

Hence the right option is A.

Note – To solve this problem we found the relation between h and x and then use the obtained relation in order to calculate angle P here we have used the values that $\tan 60 = \sqrt 3 $ and $\tan 30 = \dfrac{1}{{\sqrt 3 }}$. Doing this will solve your problem.