Question

The shaded region in the given Venn diagram represents.

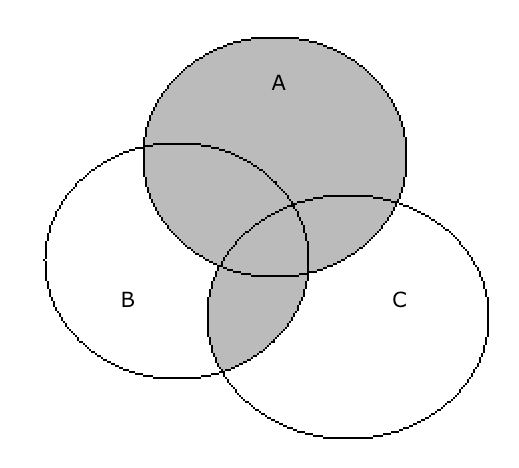
A. \[A \cap \left( {B \cap C} \right)\]
B. \[A \cup \left( {B \cup C} \right)\]
C. \[A \cap \left( {B \cup C} \right)\]
D. \[A \cup \left( {B \cap C} \right)\]

Answer 1

Hint: First we will first draw the Venn diagrams of the of the given expressions \[A \cap \left( {B \cap C} \right)\], \[A \cup \left( {B \cup C} \right)\], \[A \cap \left( {B \cup C} \right)\] and \[A \cup \left( {B \cap C} \right)\] and then check with the given diagram to find the required solution.

Complete step by step answer:

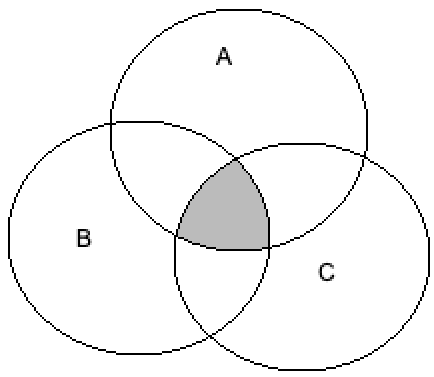
First, we will consider the option \[A \cap \left( {B \cap C} \right)\].
Rewriting the above equation using the distributive law, we get
\[ \Rightarrow A \cap \left( {B \cap C} \right) = \left( {A \cap B} \right) \cap \left( {A \cap C} \right)\]
We will draw the Venn diagram of the above equation by shading the intersection of A, B, and C, we get

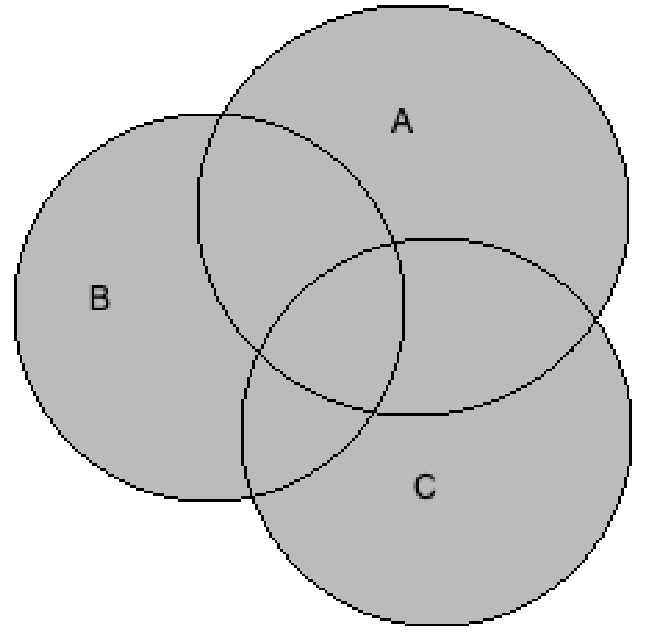
Now, we will consider the option \[A \cup \left( {B \cup C} \right)\].
Rewriting the above equation using the distributive law, we get
\[ \Rightarrow A \cup \left( {B \cup C} \right) = \left( {A \cup B} \right) \cup \left( {A \cup C} \right)\]
We will draw the Venn diagram of the above equation by shading the union of A, B, and C, we get

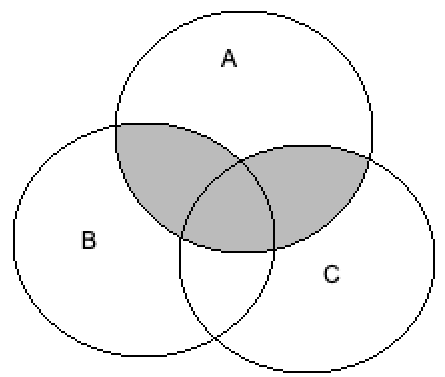
Now, we will consider the option \[A \cap \left( {B \cup C} \right)\].
Rewriting the above equation using the distributive law, we get
\[ \Rightarrow A \cap \left( {B \cup C} \right) = \left( {A \cap B} \right) \cup \left( {A \cap C} \right)\]
We will draw the Venn diagram of the above equation by shading the union of the intersection of A and B and the intersection of A and C, we get

Now, we will consider the option \[A \cup \left( {B \cap C} \right)\].
Rewriting the above equation using the distributive law, we get
\[ \Rightarrow A \cup \left( {B \cap C} \right) = \left( {A \cup B} \right) \cap \left( {A \cup C} \right)\]
We will draw the Venn diagram of the above equation by shading the intersection of the union of A and B and union of A and C, we get

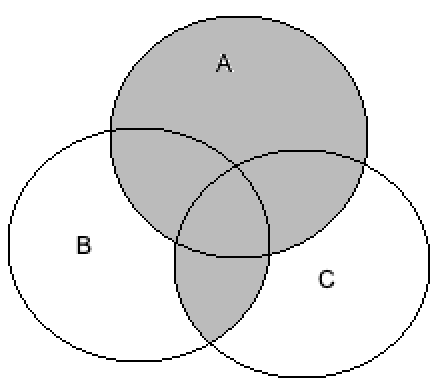
Hence, option D is correct.

Note: In solving these types of questions, students should be familiar with the making of Venn diagrams, complements, union, and intersections. One should shade the region to be selected with some different colors for a better understanding. We should be careful whiles shading the region as one may shade a different part of the diagrams, which is wrong.