Question

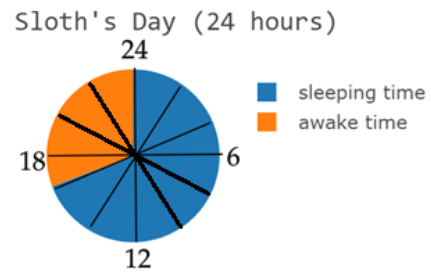
The shaded portion on a \[\text{24 hour}\] clock given below tells the sleeping time of a sloth (a bear). Find the time for which the sloth is asleep. Find the time for which the sloth is awake. If it sleeps at \[\text{6h 15min}\] then when does the sloth awake?

Answer 1

Hint: In the clocks that we use in our daily life, the markings are only up to \[\text{12 hours}\] and each division measures \[\text{5min}\] but here the markings have changed and so will the value of each division on the clock. This value of each division will be the least count of the clock and we can multiply this least count with the number of divisions used to find the total value.

Complete solution:
The entire markings on the clock represent a period of \[\text{24 hours}\] , which means that each quadrant represents \[\dfrac{\text{24 hours}}{4}=6\text{ hours}\].
Furthermore, each quadrant has three divisions, which means that the value of each division would be \[\dfrac{6\text{ hours}}{3}=2\text{ hours}\] . This is the least count of the given clock.
Now the sloth sleeps for almost three quadrants of the clock, that is, three quadrants minus one division of the clock. We know the value of a quadrant and also the value of a division, so we can say that the time for which the sloth sleeps is \[(3\times 6\text{ hours)-2 hours=16 hours}\].
We have found the sleeping time of the sloth. Now, to find the awake time of the sloth, we can simply subtract the sleeping time from the period of the entire day. Hence, the awake time of the sloth will be \[\text{(24-16)hours= 8 hours}\].

If the sloth sleeps at \[\text{6h 15min}\] , he sleeps for the next \[\text{16 hours}\] , which means the sloth will wake up at \[22\text{hours 15min}\]. We could come at the above answer by the simple addition of the sleeping time to the starting time for the sloth.

Note: An alternative way to approach this would be as follows. After finding the value of one division of the clock or the least count of the clock, we can count the number of divisions that represents the sleeping time of the sloth. There are 8 such divisions. Hence the sleeping time would be equal to eight times the value of one division, that is \[8\times 2\text{ hours}=16\text{ hours}\].