Question

The set of all points where the function $f\left( x \right) = \sqrt[3]{{{x^2}\left| x \right|}}$ is differentiable is
A) $\left[ {0,\infty } \right)$
B) $\left( {0,\infty } \right)$
C) $\left( { - \infty ,\infty } \right)$
D) $\left( { - \infty ,0} \right) \cup \left( {0,\infty } \right)$

Answer 1

Hint:
We can find the domain of the given function. Then we can split the modulus function as two functions by taking the positive and negative values of the domains. Then we can simplify the function and plot the graph of the function. From the graph, we can find the points at which the derivative doesn't exist.

Complete step by step solution:
We have the function $f\left( x \right) = \sqrt[3]{{{x^2}\left| x \right|}}$ .
As the cube root can be negative or positive, x can take any values. So, the domain of the function is real numbers.
Now we can split the modulus function across the domain.
When x is positive, modulus will become, $\left| x \right| = x$
Then the function will become,
$ \Rightarrow f\left( x \right) = \sqrt[3]{{{x^2} \times \left( x \right)}}$ , when $x \geqslant 0$
So, we have
$ \Rightarrow f\left( x \right) = \sqrt[3]{{{x^3}}}$ , when $x \geqslant 0$
On cancelling the cube and cube root, we get
$ \Rightarrow f\left( x \right) = x$ , when $x \geqslant 0$ … (1)
When x is negative, modulus will become, $\left| x \right| = - x$
Then the function will become,
$ \Rightarrow f\left( x \right) = \sqrt[3]{{{x^2} \times \left( { - x} \right)}}$ , when $x < 0$
So, we have
$ \Rightarrow f\left( x \right) = \sqrt[3]{{ - {x^3}}}$ , when $x < 0$
On cancelling the cube and cube root, we get
$ \Rightarrow f\left( x \right) = - x$ , when $x < 0$ …. (2)
On combining (1) and (2), we can write the function as
$ \Rightarrow f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
  {x\,,x \geqslant 0} \\
  { - x\,,x < 0}
\end{array}} \right.$
Now we can plot the graph of the function. When x increases, y increases in the 1^st quadrant. When x is decreasing, y increases in the 2^nd quadrant. So, the graph can be drawn as

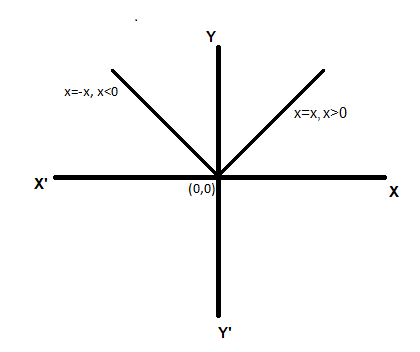
From the graph, the function is having a steep change in the slope at the origin. So, the derivative does not exist at the point $x = 0$ .
So, the derivative of the function exists at all the points except zero.
Therefore, the required interval is $\left( { - \infty ,0} \right) \cup \left( {0,\infty } \right)$ .

So, the correct answer is option D.

Note:
Alternatively,
We know that the function $f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
  {x\,,x \geqslant 0} \\
  { - x\,,x < 0}
\end{array}} \right.$ is the expansion of modulus function.
\[ \Rightarrow f\left( x \right) = \left| x \right|\]
We know that the modulus function is not differentiable at 0.
Therefore, the required interval is $\left( { - \infty ,0} \right) \cup \left( {0,\infty } \right)$ .
We must know that the open interval $\left( {a,b} \right)$ means all the points between a and b excluding the end points.