Question

The r.m.s. the value of an a.c. of 50 Hz is 10A. The time taken by the alternating current in reaching from zero to maximum value and peak value of current will be:
(A) $2 \times 10^{-2}$ s and 14.14 A
(B) $1 \times 10^{-2}$ s and 7.07 A
(C) $5 \times 10^{-3}$ s and 7.07 A
(D) $5 \times 10^{-3}$ s and 14.14 A

Answer 1

Hint: In an alternating current supply, the amplitude of the wave is the peak value of the current. The time it takes to reach from zero to peak is the time period divided by 4 as the time period is the time it takes for completion of one cycle (0 to 2$ \pi$).
Formula used:
The time period and the frequency of the a.c. current (wave ) are related as:
$f = \dfrac{1}{T}$ .
The r.m.s. value of the current and the peak value of the current are related as:
$I_{rms} = \dfrac{I_0}{\sqrt{2}}$

Complete answer:
We are given that the given a.c. current has a frequency of 50 Hz. The time period of this supply is therefore,
$T = \dfrac{1}{50} = 0.02 $ s.
The time period is the time taken for one whole wave/cycle to pass. One whole wave consists of a crest and a trough. One-fourth of this wave can be considered the distance between zero and the first peak. This is depicted below:

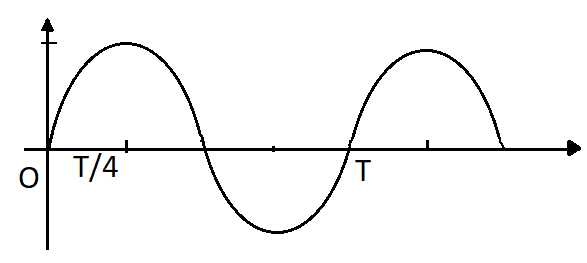
The time period also becomes one-fourth. Therefore, the required time to reach the peak, starting from zero is:
$\dfrac{T}{4} = \dfrac{0.02}{4} = 5 \times 10^{-3}$ s.
Now, the peak value of the current can be obtained from the r.m.s. value of the current as:
$I_0 = \sqrt{2} I_{rms} = \sqrt{2} \times 10 = 14.14$ A.

Therefore, the correct answer is option (D).

Note:
The unit of frequency is Hertz which is also expressed as per second. Keeping this in mind, it becomes simpler to invert the frequency to obtain the time period and obtain the frequency. There is also another term called angular frequency which is used to describe a wave. The unit of angular frequency is in rad/s.