Question

The ${\rm{C}} - {\rm{C}}$ and ${\rm{Si}} - {\rm{C}}$ inter-atomic distance are 154 pm and 188 pm. The atomic radius of ${\rm{Si}}$ is:

A.77 pm
B.94 pm
C.114 pm
D.111 pm

Answer 1

Hint:We know that the distance between nuclei of atoms within a molecule is termed as inter-atomic distance or internuclear distance. The summation of radii of the combining atoms gives the interatomic distance if the atoms are linked by a single covalent bond.

Complete step by step answer:

Let’s understand the interatomic distance with the help of a diagram.

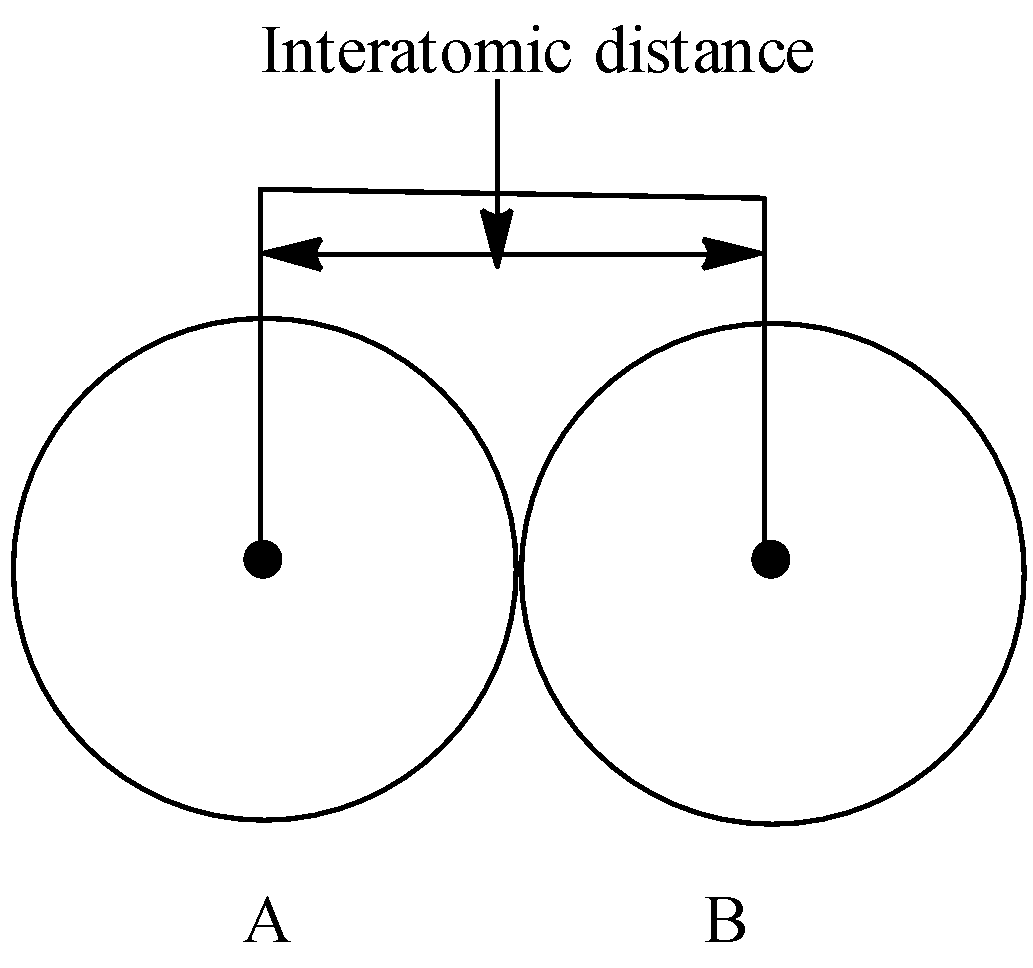
Two atoms namely A and B form a bond. The centre point indicates the nucleus of the atoms. The distance between the nuclei of two atoms is the interatomic distance.

For C-C, given interatomic distance is 154 pm and the bond is a single covalent bond. So, the summation of the radius of two carbon atoms is equal to 154 pm.

${r_{\rm{C}}} + {r_{\rm{C}}} = 154$

\[ \Rightarrow 2{r_C} = 154\]

$ \Rightarrow {r_C} = \frac{{154}}{2}$

$ \Rightarrow {r_C} = 77\,{\rm{pm}}$


Therefore, the radius of the carbon atom is 77 pm.

Next is ${\rm{Si}} - {\rm{C}}$. The given interatomic distance for ${\rm{Si}} - {\rm{C}}$ is 188 pm and the bond is a single covalent bond. That means, summation of radii of carbon atom and silicon atom is 188 pm.

  ${r_{\rm{C}}} + {r_{Si}} = 188$


In C-C bond, the atomic radii of carbon is 77 pm. So, we put the value of atomic radii of carbon in the above equation.
$ \Rightarrow {r_{Si}} + 77 = 188$

\[ \Rightarrow {r_{{\rm{Si}}}} = 188 - 77\]

$ \Rightarrow {r_{Si}} = 111\,\,{\rm{pm}}$


Therefore, the radius of the silicon atom is 111 pm.

Hence, the correct answer is option D.


Additional Information:
Atomic radius is defined as the distance from the centre of nucleus to the outermost shell containing the electrons. Atomic radius is expressed in three different forms, such as, covalent radii, van der Waals radii and metallic radii. Covalent radius is expressed as follows:

${r_{{\rm{Covalent}}}} = \frac{{{\rm{Internuclear}}\,{\rm{distance}}\,{\rm{in}}\,{\rm{the}}\,\,{\rm{bonded}}\,\,{\rm{atoms}}}}{2}$



Note:
Two atoms linked to each other by single covalent bond or by double or triple bond. In case of linking by double or triple bond, then half of inter nuclear distance does not represent the covalent radius. But in case of linking of atoms by covalent bond, the value of covalent radius is little less than actual atomic radius as covalent bond is formed by overlapping of atomic orbitals.