Question

The resultant of two vectors at angle 150${}^{\circ }$ is 10 units and is perpendicular to one vector. The magnitude of the smaller vector is
$\text{A}\text{. 10units}$
$\text{B}\text{. 10}\sqrt{3}\text{units}$
$\text{C}\text{. 10}\sqrt{2}\text{units}$
$\text{D}\text{. 5}\sqrt{3}\text{units}$

Answer 1

Hint: Use the law of Parallelogram for vectors, which gives the resultant of two vectors. The magnitude of the resultant R is given as $R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }$, where A and B is the magnitudes of the vectors $\overrightarrow{A}$ and $\overrightarrow{B}$respectively. $\theta $ is the angle between A and B.

Formula used:
$R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }$

Complete step by step answer:
The resultant vector $\overrightarrow{R}$ of two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ is given as $\overrightarrow{R}=\overrightarrow{A}+\overrightarrow{B}$. The magnitude (R) of the resultant is given as $R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }$, where A and B is the magnitudes of the vectors $\overrightarrow{A}$ and $\overrightarrow{B}$respectively. $\theta $ is the angle between A and B.
Let us first draw a figure.

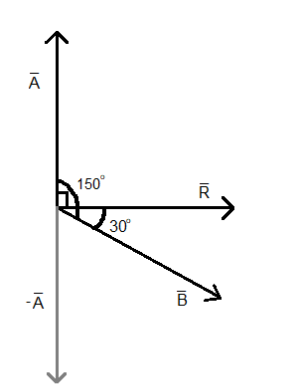
Here, $\left( -\overrightarrow{A} \right)$ is a vector, magnitude is equal to vector A but it is opposite in direction of A.
When we use the resultant formula for $\overrightarrow{R}$, $\overrightarrow{A}$ and $\overrightarrow{B}$, we get $R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }$
Here, $\theta ={{150}^{\circ }}$.
$\Rightarrow R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos (150)}$
$\cos (150)=-\dfrac{\sqrt{3}}{2}$.
$\Rightarrow R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\left( -\dfrac{\sqrt{3}}{2} \right)}$
$\Rightarrow R=\sqrt{{{A}^{2}}+{{B}^{2}}-\sqrt{3}AB}$
Square both sides.
$\Rightarrow {{R}^{2}}={{A}^{2}}+{{B}^{2}}-\sqrt{3}AB$ ……..(i).
As per the figure x$\left( -\overrightarrow{A} \right)+\overline{R}=\overline{B}$. Therefore, the magnitude of R is $B=\sqrt{{{A}^{2}}+{{R}^{2}}+2AR\cos 90}$
We know that cos90=0.
$\Rightarrow B=\sqrt{{{A}^{2}}+{{R}^{2}}+0}$
$\Rightarrow B=\sqrt{{{A}^{2}}+{{R}^{2}}}$ ……(ii).
Square both sides.
$\Rightarrow {{B}^{2}}={{A}^{2}}+{{R}^{2}}$ ……(iii).
Substitute the values of B and ${{B}^{2}}$ in equation (i).
Therefore,
$\Rightarrow {{R}^{2}}={{A}^{2}}+({{A}^{2}}+{{R}^{2}})-\sqrt{3}A\left( \sqrt{{{A}^{2}}+{{R}^{2}}} \right)$
Open the brackets.
$\Rightarrow {{R}^{2}}-{{R}^{2}}=2{{A}^{2}}-\sqrt{3}A\left( \sqrt{{{A}^{2}}+{{R}^{2}}} \right)$
$\Rightarrow 0=2{{A}^{2}}-\sqrt{3}A\left( \sqrt{{{A}^{2}}+{{R}^{2}}} \right)$
Therefore,
$2{{A}^{2}}=\sqrt{3}A\left( \sqrt{{{A}^{2}}+{{R}^{2}}} \right)$
Divide both sides by A. Therefore,
$2A=\sqrt{3}\left( \sqrt{{{A}^{2}}+{{R}^{2}}} \right)$
Square both the sides.
$4{{A}^{2}}=3\left( {{A}^{2}}+{{R}^{2}} \right)$
Open the brackets.
$4{{A}^{2}}=3{{A}^{2}}+3{{R}^{2}}$
This implies, ${{A}^{2}}=3{{R}^{2}}$.
Therefore, $A=\sqrt{3}R$.
The given value of R is 10 units. Therefore, $A=\sqrt{3}\left( 10 \right)=10\sqrt{3}units$.
Substitute the value of A in equation (iii).
$\Rightarrow {{B}^{2}}={{\left( \sqrt{3}R \right)}^{2}}+{{R}^{2}}$
$\Rightarrow {{B}^{2}}=3{{R}^{2}}+{{R}^{2}}$
$\Rightarrow {{B}^{2}}=4{{R}^{2}}$
This implies that $B=2R=2\times 10=20units$.
Therefore, the magnitudes of A and B are $10\sqrt{3}$units and 20 units respectively.
Hence, the smaller vector is $\overrightarrow{A}$ with a magnitude of $10\sqrt{3}$ units.
Therefore, the correct option is B.

Note: This problem can also be solved by resolving the vectors into their components.
Resolve vector $\overline{B}$ into horizontal components along vector $\overline{R}$ and a vertical component along vector $-\overline{A}$. The horizontal component is equal to $B\cos (60)$ and the vertical component is equal to $B\sin (60)$.
Since the $\overline{B}$ is the resultant of $-\overline{A}$ and $\overline{R}$, $B\cos (60)=R$ and $B\sin (60)=A$.
Therefore, $B=\dfrac{R}{\cos 60}$.
$\cos (60)=\dfrac{1}{2}$ and R=10units.
$\Rightarrow B=\dfrac{R}{\left( \dfrac{1}{2} \right)}=2R=2\times 10=20units$
We also have $B\sin (60)=A$. Substitute the value of B.
Therefore, $A=(20).\left( \dfrac{\sqrt{3}}{2} \right)=10\sqrt{3}units$
Therefore, the smaller vector is $\overline{A}$ and its magnitude is $10\sqrt{3}units$.