Question

The resultant of two forces P and Q is R. If R is doubled and if Q is reversed; R is again doubled. Then ${{P}^{2}}:{{Q}^{2}}:{{R}^{2}}$ is given by,
A. 2 : 2 : 3
B. 3 : 2 : 2
C. 2 : 3 : 2
D. 2 : 3 : 1

Answer 1

Hint:In order to solve this question, we should have some knowledge of vector formulas like, ${{\left| R \right|}^{2}}={{\left| P \right|}^{2}}+{{\left| Q \right|}^{2}}+2\left| P \right|\left| Q \right|\cos \theta $. Also, we need to know that if vector Q changes its direction, then it becomes -Q. If Q is doubled, then it becomes 2Q. Also, if the vector is reversed, and if angle is $\theta $ with another vector, then it becomes $180-\theta $. By using these properties, we can solve this question.

Complete step-by-step answer:
In this question, we have been given that resultant of two forces P and Q is R and few conditions are given for P, Q and R. And we have been asked to find the value of ${{P}^{2}}:{{Q}^{2}}:{{R}^{2}}$. To solve this, we know that the resultant of two vectors is related with them as, ${{\left| R \right|}^{2}}={{\left| P \right|}^{2}}+{{\left| Q \right|}^{2}}+2\left| P \right|\left| Q \right|\cos \theta $.

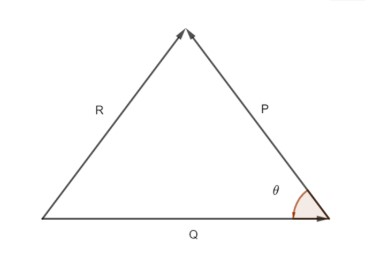
Here, we have considered the angle between vector P and vector Q as $\theta $. So, according to the formula, we can say,
${{\left| R \right|}^{2}}={{\left| P \right|}^{2}}+{{\left| Q \right|}^{2}}+2\left| P \right|\left| Q \right|\cos \theta \ldots \ldots \ldots \left( i \right)$
Now, we have been given that if Q is doubled, then R is doubled. So, we can write as,
$\left| {{\left( 2R \right)}^{2}} \right|={{\left| P \right|}^{2}}+\left| {{\left( 2Q \right)}^{2}} \right|+2\left| P \right|\left| 2Q \right|\cos \theta $
And we can write it further as,
$4{{\left| R \right|}^{2}}={{\left| P \right|}^{2}}+4{{\left| Q \right|}^{2}}+4\left| P \right|\left| Q \right|\cos \theta \ldots \ldots \ldots \left( ii \right)$
We have been also given that if Q is reversed, then R is again doubled. So, we will write Q as -Q and $\theta $ as $180-\theta $ and R as 2R. So, we get,
$\left| {{\left( 2R \right)}^{2}} \right|={{\left| P \right|}^{2}}+{{\left| -Q \right|}^{2}}+2\left| P \right|\left| -Q \right|\cos \left( 180-\theta \right)$
And we can further write it as,
$4{{\left| R \right|}^{2}}={{\left| P \right|}^{2}}+{{\left| Q \right|}^{2}}+2\left| P \right|\left| Q \right|\cos \left( 180-\theta \right)$
Now, we know that $\cos \left( 180-\theta \right)=-\cos \theta $. So, we get the equation as,
$4{{\left| R \right|}^{2}}={{\left| P \right|}^{2}}+{{\left| Q \right|}^{2}}-2\left| P \right|\left| Q \right|\cos \theta \ldots \ldots \ldots \left( iii \right)$
Now, we will subtract equation (iii) from equation (ii). So, we get,
$4{{\left| R \right|}^{2}}-4{{\left| R \right|}^{2}}={{\left| P \right|}^{2}}-{{\left| P \right|}^{2}}+4{{\left| Q \right|}^{2}}-{{\left| Q \right|}^{2}}+4\left| P \right|\left| Q \right|\cos \theta +2\left| P \right|\left| Q \right|\cos \theta $
And we can further write it as,
$\begin{align}
  & 0=0+3{{\left| Q \right|}^{2}}+6\left| P \right|\left| Q \right|\cos \theta \\
 & \Rightarrow 3{{\left| Q \right|}^{2}}=-6\left| P \right|\left| Q \right|\cos \theta \\
 & \Rightarrow \left| Q \right|=-2\left| P \right|\cos \theta \ldots \ldots \ldots \left( iv \right) \\
\end{align}$
Now, we will square both sides of the equation. So, we get,
${{\left| Q \right|}^{2}}=4{{\left| P \right|}^{2}}{{\cos }^{2}}\theta \ldots \ldots \ldots \left( v \right)$
Now we will subtract equation (i) from equation (iii). So, we get,
$4{{\left| R \right|}^{2}}-{{\left| R \right|}^{2}}={{\left| P \right|}^{2}}-{{\left| P \right|}^{2}}+{{\left| Q \right|}^{2}}-{{\left| Q \right|}^{2}}-2\left| P \right|\left| Q \right|\cos \theta -2\left| P \right|\left| Q \right|\cos \theta $
And we can further write it as,
$3{{\left| R \right|}^{2}}=-4\left| P \right|\left| Q \right|\cos \theta $
And form equation (iv), we will put the value of $\left| Q \right|$. So, we get,
$\begin{align}
  & 3{{\left| R \right|}^{2}}=-4\left| P \right|\left( -2\left| P \right|\cos \theta \right)\cos \theta \\
 & \Rightarrow 3{{\left| R \right|}^{2}}=8{{\left| P \right|}^{2}}{{\cos }^{2}}\theta \\
 & \Rightarrow {{\left| R \right|}^{2}}=\dfrac{8}{3}{{\left| P \right|}^{2}}{{\cos }^{2}}\theta \ldots \ldots \ldots \left( vi \right) \\
\end{align}$
Now, we will put the values of ${{\left| R \right|}^{2}},{{\left| Q \right|}^{2}},\left| Q \right|$ from equations (vi), (v) and (iv) to equation (i). So, we get,
$\begin{align}
  & \dfrac{8}{3}{{\left| P \right|}^{2}}{{\cos }^{2}}\theta ={{\left| P \right|}^{2}}+4{{\left| P \right|}^{2}}{{\cos }^{2}}\theta +2\left| P \right|\left( -2\left| P \right|\cos \theta \right)\cos \theta \\
 & \Rightarrow \dfrac{8}{3}{{\left| P \right|}^{2}}{{\cos }^{2}}\theta ={{\left| P \right|}^{2}}+4{{\left| P \right|}^{2}}{{\cos }^{2}}\theta -4{{\left| P \right|}^{2}}{{\cos }^{2}}\theta \\
 & \Rightarrow {{\left| P \right|}^{2}}=\dfrac{8}{3}{{\left| P \right|}^{2}}{{\cos }^{2}}\theta \ldots \ldots \ldots \left( vii \right) \\
\end{align}$
Now, if the ratio of ${{P}^{2}}:{{Q}^{2}}:{{R}^{2}}$ is there, then we get,
$\dfrac{8}{3}{{\left| P \right|}^{2}}{{\cos }^{2}}\theta :4{{\left| P \right|}^{2}}{{\cos }^{2}}\theta :\dfrac{8}{3}{{\left| P \right|}^{2}}{{\cos }^{2}}\theta $
Which is the same as,
$\begin{align}
  & 8{{\left| P \right|}^{2}}{{\cos }^{2}}\theta :2{{\left| P \right|}^{2}}{{\cos }^{2}}\theta :8{{\left| P \right|}^{2}}{{\cos }^{2}}\theta \\
 & \Rightarrow 2:3:2 \\
\end{align}$
Hence, the ratio of ${{P}^{2}}:{{Q}^{2}}:{{R}^{2}}$ is $2:3:2$. Therefore, option C is the correct answer.

Note: While solving this question, we need to remember a vector formula, ${{\left| R \right|}^{2}}={{\left| P \right|}^{2}}+{{\left| Q \right|}^{2}}+2\left| P \right|\left| Q \right|\cos \theta $. Then we will use the given condition to get the values of ${{R}^{2}},{{Q}^{2}},{{P}^{2}}$ in terms of any one vector to get the ratio and then we will simplify to get the answer. The probable mistake we can make here is not considering the angle as $\cos \left( 180-\theta \right)$ and then we will get the incorrect result.