Question

The resultant of two forces has a magnitude of $20N$. If one of the forces of magnitude $20\sqrt{3}N$ and makes an angle of ${{30}^{o}}$ with the resultant then, the other force must be of magnitude
(A). $10\sqrt{3}N$
(B). $20N$
(C). $20\sqrt{3}N$
(D). $10N$

Answer 1

Hint: Two vectors are added such that their resultant makes angle ${{30}^{o}}$ with one of the vectors. The magnitude of a vector is the absolute value of the vector. The sum of the vectors gives the resultant, so, the resultant subtracted by a vector gives the other vector. Squaring both sides of the equation, the magnitude of other vectors can be calculated.
Formula used:
${{B}^{2}}={{R}^{2}}+{{A}^{2}}-2RA\cos 30$

Complete answer:
Quantities that possess magnitude as well as direction as known as vectors. They are represented in space by magnitude and direction.
Vectors can be added by different laws; one of them is the parallelogram law of addition. It states that when two vectors taken in different order such that they form the sides of a parallelogram, then their resultant is the diagonal between the sides.

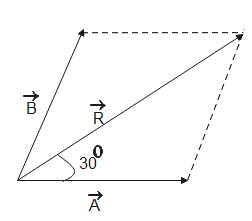
$\vec{R}$ is the resultant sum of $\vec{A}$ and $\vec{B}$. Therefore,
$\begin{align}
  & \vec{A}+\vec{B}=\vec{R} \\
 & \Rightarrow \vec{B}=\vec{R}-\vec{A} \\
\end{align}$
Squaring on both sides, we get,
${{B}^{2}}={{R}^{2}}+{{A}^{2}}-2RA\cos 30$
Given, $\vec{R}=20N$, $\vec{A}=20\sqrt{3}N$, angle between $\vec{A},\,\vec{R}$ is ${{30}^{o}}$
Substituting given values in the above equation, we get,
$\begin{align}
  & {{B}^{2}}={{(20)}^{2}}+{{(20\sqrt{3})}^{2}}-2\times 20\times 20\sqrt{3}\cos 30 \\
 & \Rightarrow {{B}^{2}}=400+1200-2\times 400\sqrt{3}\times \dfrac{\sqrt{3}}{2} \\
 & \Rightarrow {{B}^{2}}=400+1200-1200 \\
 & \Rightarrow {{B}^{2}}=400 \\
 & \therefore B=20N \\
\end{align}$
Therefore, the magnitude of $\vec{B}$ is $20N$.
Therefore, the force must be of magnitude $20N$.

Hence, the correct option is (B).

Additional Information:
The vectors can also be multiplied in two ways. The vector product or cross product of two vectors gives a vector as resultant. It is calculated as $\vec{a}\times \vec{b}=ab\sin \theta \hat{n}$ ($\hat{n}$ is a unit vector perpendicular to the two vectors). The scalar or dot product of two vectors gives a scalar quantity as resultant. It is calculated as $\vec{a}\cdot \vec{b}=ab\cos \theta $.

Note:
The other type of quantity is scalar, it has only magnitude represented by its unit. The vectors can also be added by triangle law of vector addition, the parallelogram of vector addition etc. The vectors can also be multiplied and the resultant product of vectors can either be a scalar or a vector.