Question

The resistance in the four arms of a Wheatstone network in cyclic order is $5\Omega ,2\Omega ,6\Omega $ and $15\Omega ,$ If the current of 2.8 A enters the junction of $5\Omega $ and $15\Omega $ , then the current through $2\Omega $ resistor is
(A). 1.5 A
(B). 28 A
(C). 0.7 A
(D). 1.4 A
(E). 2.1 A

Answer 1

- Hint: In order to solve this problem, we will use the basic concept of resistor solving and the most important concept of Wheatstone bridge which is used for measuring the value of unknown resistance. When the current through the null of Wheatstone bridge is zero then the bridge is said to be balanced and at that time we will calculate the current through the 2 ohm resistor.

Formula used- Condition for balanced bridge
$\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{R_3}}}{{{R_4}}}$

Complete step-by-step solution -

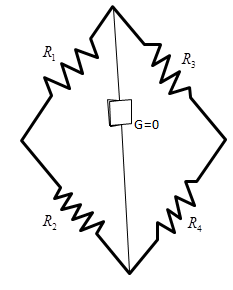
Given values of the resistance
${R_1} = 5\Omega ,{R_2} = 15\Omega ,{R_3} = 2\Omega ,{R_4} = 6\Omega $
Substituting these values in the condition for checking whether the bridge is balanced or not
\[
   \Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{R_3}}}{{{R_4}}} \\
   \Rightarrow \dfrac{5}{{15}} = \dfrac{2}{6} \\
\]
Hence the bridge is balanced.
As we know when the bridge is balanced, the current through the galvanometer coil of a wheatstone bridge is zero and all current flows through two parallel paths as shown in the below figure.

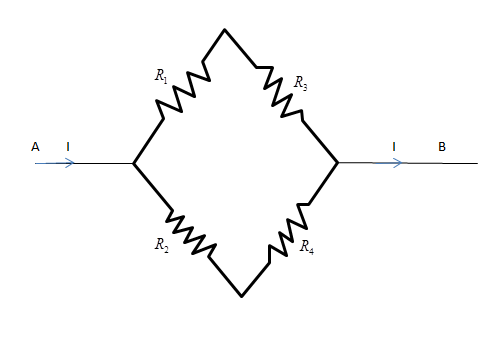
Since we have to find the current through 2 ohm resistor i.e. ${R_3}$ resistor
Since current of 2.8 A enters through junction A, now we will use the current division rule to find the current through 2 ohm resistor.
As we know $\left[ {{I_{2\Omega }} = I\dfrac{{{R_2} + {R_4}}}{{{R_1} + {R_3} + {R_2} + {R_4}}}} \right]$
Substituting the values of resistor and current in the above equation we get
$
  {I_{2\Omega }} = I\dfrac{{{R_2} + {R_4}}}{{{R_1} + {R_3} + {R_2} + {R_4}}} \\
  {I_{2\Omega }} = 2.8 \times \dfrac{{15 + 6}}{{5 + 2 + 15 + 6}} \\
  {I_{2\Omega }} = 2.8 \times \dfrac{{21}}{{28}} = 2.1\Omega \\
  {I_{2\Omega }} = 2.1\Omega \\
 $
Hence, the correct option is “E”.

Note- Wheatstone bridge is used to find low resistance and is now also used is electronics appliances to measure temperature, strain etc. To solve these types of numerical first you need to have a good concept of resistance network solving problems and have a concept of current and voltage division rules.