
The remainder when ${{27}^{40}}$ is divide by 12 is
(a) 3
(b) 7
(c) 9
(d) 11
Answer
600.3k+ views
Hint: First, we have to simplify ${{27}^{40}}$ in the reduced form that we will get as \[{{\left( {{3}^{3}} \right)}^{40}}\] . Then we have to use the concept of binomial expansion using the formula ${{\left( a+b \right)}^{n}}=\sum\limits_{r=0}^{n}{{{\left( a \right)}^{n-r}}{{\left( b \right)}^{r}}}\times {}^{n}{{C}_{r}}$ . So, for a and b we can write 3 in the form of \[\left( 4-1 \right)\] . And at last on solving the expansion, we will have the final answer in the form of \[dividend=divisor\cdot quotient+remainder\] . Thus, we will get our required answer.
Complete step-by-step answer:
Here, we can write a simplified form of ${{27}^{40}}$ i.e. $27=3\times 3\times 3={{3}^{3}}$ . So, we can write ${{27}^{40}}={{\left( {{3}^{3}} \right)}^{40}}={{3}^{120}}$ .
Now, we can write ${{3}^{120}}$ as $3\times {{3}^{119}}$ . Also, we can simplify ${{3}^{119}}$ in the form of binomial expansion form i.e. ${{\left( 4-1 \right)}^{119}}$ . So, we will expand this using binomial expansion given as ${{\left( a+b \right)}^{n}}=\sum\limits_{r=0}^{n}{{{\left( a \right)}^{n-r}}{{\left( b \right)}^{r}}}\times {}^{n}{{C}_{r}}$ .
We will use this expansion and taking $a=4,b=-1,n=119$ we can write it as
${{\left( 4-1 \right)}^{119}}=\sum\limits_{r=0}^{119}{{{\left( 4 \right)}^{119-r}}{{\left( -1 \right)}^{r}}}\times {}^{119}{{C}_{r}}$
On expanding this expression, we get
$\begin{align}
& ={{\left( 4 \right)}^{119}}{{\left( -1 \right)}^{0}}\times {}^{119}{{C}_{0}}+{{\left( 4 \right)}^{118}}{{\left( -1 \right)}^{1}}\times {}^{119}{{C}_{1}}+ \\
& {{\left( 4 \right)}^{117}}{{\left( -1 \right)}^{2}}\times {}^{119}{{C}_{2}}+.....+{{\left( 4 \right)}^{1}}{{\left( -1 \right)}^{118}}\times {}^{119}{{C}_{118}}+ \\
& {{\left( 4 \right)}^{0}}{{\left( -1 \right)}^{119}}\times {}^{119}{{C}_{119}} \\
\end{align}$
On simplifying terms, we get
\[={{\left( 4 \right)}^{119}}\times {}^{119}{{C}_{0}}-{{\left( 4 \right)}^{118}}\times {}^{119}{{C}_{1}}+{{\left( 4 \right)}^{117}}\times {}^{119}{{C}_{2}}+.....+\left( 4 \right)\times {}^{119}{{C}_{118}}-1\]
(using \[{}^{n}{{C}_{n}}=1\] )
Now, from above equation taking 4 common from expansion, we get
\[=4\left( {{\left( 4 \right)}^{118}}\times {}^{119}{{C}_{0}}-{{\left( 4 \right)}^{117}}\times {}^{119}{{C}_{1}}+{{\left( 4 \right)}^{116}}\times {}^{119}{{C}_{2}}+.....+{}^{119}{{C}_{118}} \right)-1\]
We know that on solving the bracket terms, we will get integer value so, we will assume that whole bracket as constant term let say c. So, we will get
\[{{\left( 4 \right)}^{118}}\times {}^{119}{{C}_{0}}-{{\left( 4 \right)}^{117}}\times {}^{119}{{C}_{1}}+{{\left( 4 \right)}^{116}}\times {}^{119}{{C}_{2}}+.....+{}^{119}{{C}_{118}}=c\]
\[{{\left( 4-1 \right)}^{119}}={{3}^{119}}=4\left( c \right)-1\] ………………………(1)
So, substituting this value of equation (1) in \[{{3}^{120}}=3\times {{3}^{119}}\] we get
\[{{3}^{120}}=3\times {{3}^{119}}=3\times \left( 4\left( c \right)-1 \right)\]
On multiplying the brackets, we get
\[{{3}^{120}}=12c-3\]
Now, we have to split \[-3\] as \[-3=-12+9\] . So, on putting this value, we get
\[{{3}^{120}}=12c-12+9\]
Taking 12 common from first two terms, we get
\[{{3}^{120}}=12\left( c-1 \right)+9\]
So, this is in the form of \[dividend=divisor\cdot quotient+remainder\]
Thus, we have remainder 9 when ${{27}^{40}}$ is divided by 12.
Hence, option (c) is correct.
Note: Another approach and simple way to find remainder is taking odd and even power of 3 and dividing it by 12 and checking the remainder. So, if we take \[{{\left( {{3}^{3}} \right)}^{40}}\] then dividing 27 by 12, we get remainder as 3.
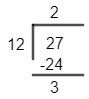
And when we take even power i.e. ${{3}^{4}}=81$ on dividing it by 12 we get remainder as 9.
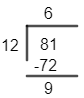
So, here we have ${{27}^{40}}={{3}^{120}}$ so 120 is even power hence the remainder will be 9 when divided by 12.
Complete step-by-step answer:
Here, we can write a simplified form of ${{27}^{40}}$ i.e. $27=3\times 3\times 3={{3}^{3}}$ . So, we can write ${{27}^{40}}={{\left( {{3}^{3}} \right)}^{40}}={{3}^{120}}$ .
Now, we can write ${{3}^{120}}$ as $3\times {{3}^{119}}$ . Also, we can simplify ${{3}^{119}}$ in the form of binomial expansion form i.e. ${{\left( 4-1 \right)}^{119}}$ . So, we will expand this using binomial expansion given as ${{\left( a+b \right)}^{n}}=\sum\limits_{r=0}^{n}{{{\left( a \right)}^{n-r}}{{\left( b \right)}^{r}}}\times {}^{n}{{C}_{r}}$ .
We will use this expansion and taking $a=4,b=-1,n=119$ we can write it as
${{\left( 4-1 \right)}^{119}}=\sum\limits_{r=0}^{119}{{{\left( 4 \right)}^{119-r}}{{\left( -1 \right)}^{r}}}\times {}^{119}{{C}_{r}}$
On expanding this expression, we get
$\begin{align}
& ={{\left( 4 \right)}^{119}}{{\left( -1 \right)}^{0}}\times {}^{119}{{C}_{0}}+{{\left( 4 \right)}^{118}}{{\left( -1 \right)}^{1}}\times {}^{119}{{C}_{1}}+ \\
& {{\left( 4 \right)}^{117}}{{\left( -1 \right)}^{2}}\times {}^{119}{{C}_{2}}+.....+{{\left( 4 \right)}^{1}}{{\left( -1 \right)}^{118}}\times {}^{119}{{C}_{118}}+ \\
& {{\left( 4 \right)}^{0}}{{\left( -1 \right)}^{119}}\times {}^{119}{{C}_{119}} \\
\end{align}$
On simplifying terms, we get
\[={{\left( 4 \right)}^{119}}\times {}^{119}{{C}_{0}}-{{\left( 4 \right)}^{118}}\times {}^{119}{{C}_{1}}+{{\left( 4 \right)}^{117}}\times {}^{119}{{C}_{2}}+.....+\left( 4 \right)\times {}^{119}{{C}_{118}}-1\]
(using \[{}^{n}{{C}_{n}}=1\] )
Now, from above equation taking 4 common from expansion, we get
\[=4\left( {{\left( 4 \right)}^{118}}\times {}^{119}{{C}_{0}}-{{\left( 4 \right)}^{117}}\times {}^{119}{{C}_{1}}+{{\left( 4 \right)}^{116}}\times {}^{119}{{C}_{2}}+.....+{}^{119}{{C}_{118}} \right)-1\]
We know that on solving the bracket terms, we will get integer value so, we will assume that whole bracket as constant term let say c. So, we will get
\[{{\left( 4 \right)}^{118}}\times {}^{119}{{C}_{0}}-{{\left( 4 \right)}^{117}}\times {}^{119}{{C}_{1}}+{{\left( 4 \right)}^{116}}\times {}^{119}{{C}_{2}}+.....+{}^{119}{{C}_{118}}=c\]
\[{{\left( 4-1 \right)}^{119}}={{3}^{119}}=4\left( c \right)-1\] ………………………(1)
So, substituting this value of equation (1) in \[{{3}^{120}}=3\times {{3}^{119}}\] we get
\[{{3}^{120}}=3\times {{3}^{119}}=3\times \left( 4\left( c \right)-1 \right)\]
On multiplying the brackets, we get
\[{{3}^{120}}=12c-3\]
Now, we have to split \[-3\] as \[-3=-12+9\] . So, on putting this value, we get
\[{{3}^{120}}=12c-12+9\]
Taking 12 common from first two terms, we get
\[{{3}^{120}}=12\left( c-1 \right)+9\]
So, this is in the form of \[dividend=divisor\cdot quotient+remainder\]
Thus, we have remainder 9 when ${{27}^{40}}$ is divided by 12.
Hence, option (c) is correct.
Note: Another approach and simple way to find remainder is taking odd and even power of 3 and dividing it by 12 and checking the remainder. So, if we take \[{{\left( {{3}^{3}} \right)}^{40}}\] then dividing 27 by 12, we get remainder as 3.
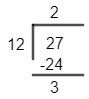
And when we take even power i.e. ${{3}^{4}}=81$ on dividing it by 12 we get remainder as 9.
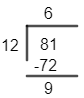
So, here we have ${{27}^{40}}={{3}^{120}}$ so 120 is even power hence the remainder will be 9 when divided by 12.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




