Question

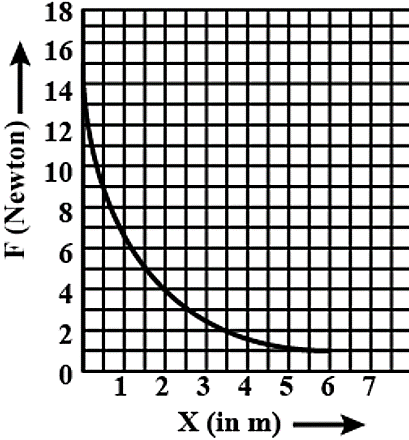
The relation between the displacement by the application of the variable force F is represented by a graph shown in the figure. If the object undergoes a displacement from X=0.5 m to X=2.5 m the work done will be approximately equal to

A. 16 J
B. 32 J
C. 1.6 J
D. 8 J

Answer 1

Hint: By looking at the graph we can say, the work done by the object for displacement from X=0.5 m to X=2.5 m will be equal to the area under the curve. Draw lines from initial point of displacement and final point of displacement which are parallel to the force axis. This gives two intersecting points on the curve. These two parallel lines together with the X-axis and curve form a trapezium. So, the work done will be equal to the area of trapezium. So, use the formula for area of trapezium and find the area. This will be the value of work done.

Formula used:
$W= F.x$
$A= \dfrac {1}{2} \times sum\quad of\quad two\quad parallel\quad lines\times distance\quad between\quad the\quad parallel\quad lines$

Complete answer:
Given: Initial position ${X}_{initial}$= 0.5 m
            Final position ${X}_{final}$= 2.5 m
We know, work done is given by,
$W= F.x$ …(1)
Where, F is the force
            x is the displacement
So, from graph and equation. (1) We can say, the work done by the object for displacement from X=0.5 m to X=2.5 m will be equal to the area under the curve.
If we draw lines from X= 0.5 m and X=2.5 m parallel to the Y-axis then we get the graph as shown below.

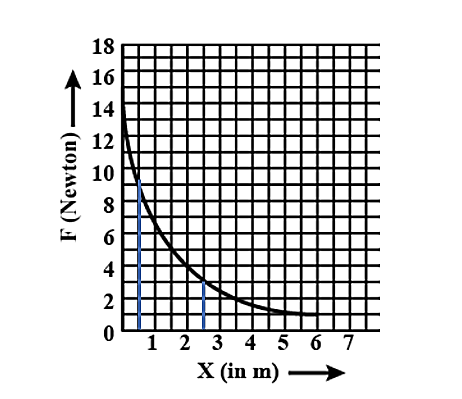
From the graph, we can see that the line from X=0.5 m intersects the curve at F= 9 Newton and the line from X=2.5 m intersects the curve at F= 3 Newton.
$\Rightarrow { F }_{ 0.5 }=9Newton$ and ${ F }_{ 2.5 }=3Newton$
We can also infer that these two parallel lines, curve and the X-axis together form a shape of a trapezium.
Thus, the work done will be,
$W= Area \quad of \quad a \quad trapezium$ …(2)
Area of a trapezium is given by,
$A= \dfrac {1}{2} \times sum\quad of\quad two\quad parallel\quad lines\times distance\quad between\quad the\quad parallel\quad lines$
$A= \dfrac {1}{2} \times \left( { F }_{ 0.5 }+{ F }_{ 2.5 } \right) \times \left( { X }_{ final }-{ X }_{ initial } \right)$
Substituting values in above equation we get,
$A= \dfrac {1}{2} \times \left( 9+3 \right) \times \left( 2.5-0.5 \right)$
$\Rightarrow A= \dfrac {1}{2} \times 12 \times 2$
$\Rightarrow A= 12$
Substituting this value in the equation. (2) we get,
$W= 12 J$
But, the area under the curve is not actually a trapezium, the work done will be greater than 12 J.
$W \approx 16J$
Thus, if the object undergoes a displacement from X=0.5 m to X=2.5 m the work done will be approximately equal to 16 J.

So, the correct answer is option A i.e. 16 J.

Note:
Work done by variable forces are bit complex. In case of a variable force, the magnitude and direction of force can change at any point of time during the work. Most of the work that we perform in our day-to-day life is an example of variable force work. Work done is highly dependent on the displacement of a body no matter how much force is applied. If the displacement is zero then the work done remains zero.