Question

The reflection of the $x = 1$ in the line $x + y = 1$ is
A. $x = 0$
B. $x + y = - 1$
C. $x - y = - 1$
D. $y = 0$

Answer 1

Hint:
Firstly, we shall draw a perpendicular on the line $x + y = 1$. Determine an arbitrary P point on the line $x = 1$ on a point Q on the perpendicular. Now the point R at which the perpendicular intersects the line $x + y = 1$ shall be the midpoint of line segment PQ. Now, assume the coordinates of the points P and R from the given information. Using these, find the coordinates of point Q. Use the condition of orthogonal lines and property of midpoint to evaluate the coordinates of point Q. Then you shall find your answer.

Complete step by step solution:
Firstly, construct a perpendicular PQ of the line $x + y = 1$ , such that point P is at the intersection of lines $x + y = 1$ and $x = 1$ . Also, Q $({x_1},{y_1})$ be an arbitrary point on PQ.

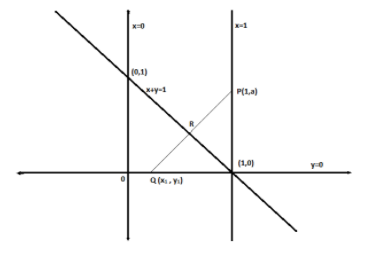
According to Question the point P lies on $x = 1$. So, let’s assume the arbitrary coordinates of P be $(1,a)$
Also, since we need to find reflection of the line we must find the image of the P $(1,a)$ .
Let’s assume the image of P be Q $({x_1},{y_1})$. Also, the point of intersection of the PQ and the line $x + y = 1$ be R. Since Q is the image of P, this means that R is the midpoint of PQ. Since R lies on the $x + y = 1$, the coordinates of general point R are given by $(x,1 - x)$
Now, let’s find the Direction Ratios of the perpendicular line segment PR.
Direction Ratios of PR are given by $(x - 1,1 - x - a)$
Direction Ratios of $x + y = 1$ are given by $(1, - 1)$
Now, Since PR is perpendicular to $x + y = 1$ the dot product of their Direction Ratios is 0
$
  1.(x - 1) - 1(1 - x - a) = 0 \\
   \Rightarrow 2x - 2 + a = 0 \\
   \Rightarrow x = 1 - \dfrac{a}{2} \\
$
There the coordinates of R are $(x,1 - x) \Rightarrow (1 - \dfrac{a}{2},\dfrac{a}{2})$
Now, we have already established that R is the midpoint of PQ, So, the coordinates of point Q $({x_1},{y_1})$ are given by
$\dfrac{{{x_1} + 1}}{2} = 1 - \dfrac{a}{2}$ and $\dfrac{{{y_1} + a}}{2} = \dfrac{a}{2}$
${x_1} = 1 - a$ and ${y_1} = 0$
As point P is arbitrary hence ${x_1}$ is also arbitrary. This means Q can be any point in the form of $(x,0)$ which represents x-axis. The equation for x-axis is $y = 0$ .

Hence, the correct option is D.

Note:
The important thing to remember is that the distance of the image and the object from the mirror is always equal. Visualizations and rough sketches are necessary while attempting such types of questions.