Question

The rectangular yard contains two flower beds in the shape of congruent isosceles right triangles. The remaining portion is a yard of trapezoidal shape whose parallel sides have lengths 15 m and 25 m. What fraction of the yard is occupied by the flower bed?

Answer 1

Hint: First of all find the length of the segments DF and EC by subtracting the given length of EF from AB and then dividing by 2. In the next step find the length of sides AD and BC to get the breadth of the rectangle. These sides will be equal to DF or EC. Now, find the area of the rectangular field by using the formula: Area = $l\times b$ considering the length (l) as AB and breadth (b) as BC. Also, find the area of the two isosceles triangles using the formula: Area = $\dfrac{{{a}^{2}}}{2}$ where (a) is the length of the equal sides of the triangle. Add the areas of the two triangles and divide it with the area of the triangle to the answer.

Complete step by step solution:
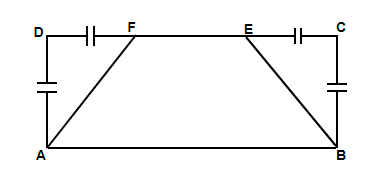
Here we have been provided with a rectangular yard in which two flower beds are present in the form of congruent isosceles right angle triangles. We have been asked to find the fraction of the yard that the flower bed occupies. To do so we need to consider the ratio of their areas.
Now, we need to find the areas of the rectangle and the triangles, so we must know the length of the equal sides of the isosceles triangle which is also the breadth of the rectangle. Let us consider the length of the rectangle as l and its breadth as b, this breadth of the rectangle forms the sides of the two congruent triangles. So we have,
(i) In the rectangle ABCD:
AB = CD = l, AD = BC = b
(ii) In the triangles ADF and BCE:
BC = CE = AD = DF = b (both the triangles are congruent and isosceles triangles have two sides equal)
In the question it is given that the length of parallel sides of the trapezoid ABEF is 15 m and 25 m, so we have,
AB = 25 m and EF = 15 m
$\begin{align}
  & \Rightarrow AB-EF=25-15 \\
 & \Rightarrow AB-EF=10 \\
\end{align}$
Since AB = CD (opposite sides of a rectangle) so we can write the above relation as:
$\begin{align}
  & \Rightarrow CD-EF=10 \\
 & \Rightarrow CE+FD=10 \\
\end{align}$
Substituting the assumed variables for these sides we get,
$\begin{align}
  & \Rightarrow b+b=10 \\
 & \Rightarrow 2b=10 \\
 & \Rightarrow b=5 \\
\end{align}$
We know that the area of a rectangle is given as Area = $l\times b$ where we have l = 25 m and b = 5 m. let us denote the area with A, so we get,
$\begin{align}
  & \Rightarrow A=25\times 5 \\
 & \Rightarrow A=125{{m}^{2}} \\
\end{align}$
$\Rightarrow $ Area of the yard = 125 ${{m}^{2}}$
Further, the area of an isosceles triangle is given as Area = $\dfrac{{{a}^{2}}}{2}$ where (a) is the length of the equal sides of the triangle. Here we have the equal sides as b = 5, denoting the area with A’ we get,
$\begin{align}
  & \Rightarrow A'=\dfrac{{{5}^{2}}}{2} \\
 & \Rightarrow A'=\dfrac{25}{2}{{m}^{2}} \\
\end{align}$
The above relation denotes the area of one flowed bed and we have two, so multiplying A’ with 2 we get,
$\Rightarrow 2A'=25{{m}^{2}}$
$\Rightarrow $ Area of the two flower beds = 25 ${{m}^{2}}$

Therefore, the fraction of the total yard occupied by the flower bed = $\dfrac{25}{125}=\dfrac{1}{5}$.

Note: Remember the properties of rectangles and isosceles triangles to solve the above question. Do not forget to multiply the area of one flower bed with 2 otherwise you will get the fraction $\dfrac{1}{10}$ which will be a wrong answer as we have two flower beds. Note that the formula of the area of an isosceles right triangle is derived from the general formula of the area of any right triangle given as Area = $\dfrac{1}{2}\times $ base $\times $ height, where the length of the base and height are equal in case of isosceles right triangle.