Question

The rectangular wire frame, shown in figure, has a width $ d $ , mass $ m $ , resistance $ R $ , and a large length. A uniform magnetic field $ B $ exists to the left of the frame. A constant force $ F $ pushing the frame into the magnetic field at $ t=0 $
(A) Find the acceleration of the frame when its speed has increased to $ v $ .
(B) Find the terminal velocity of the loop.
(C) Find the velocity at time $ t $ .

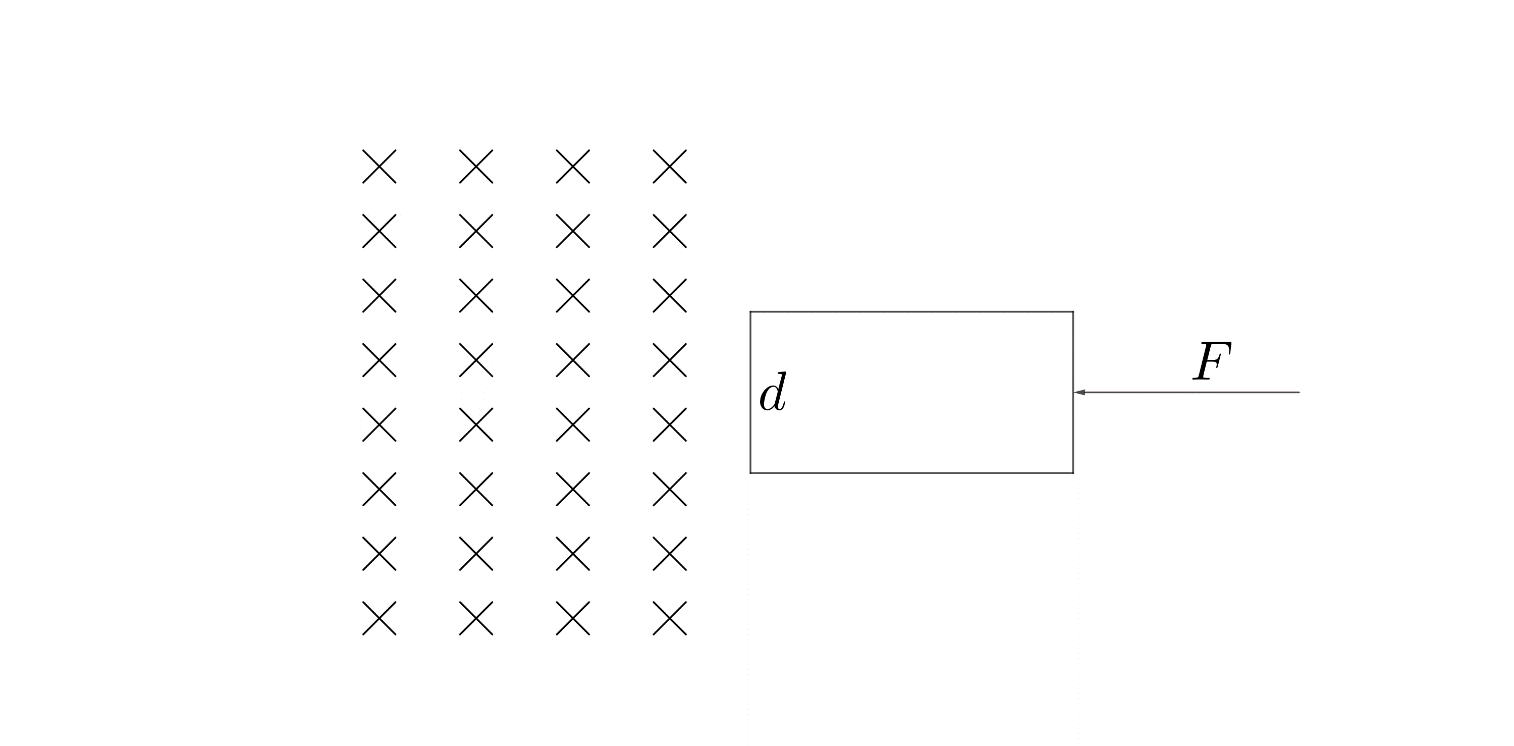
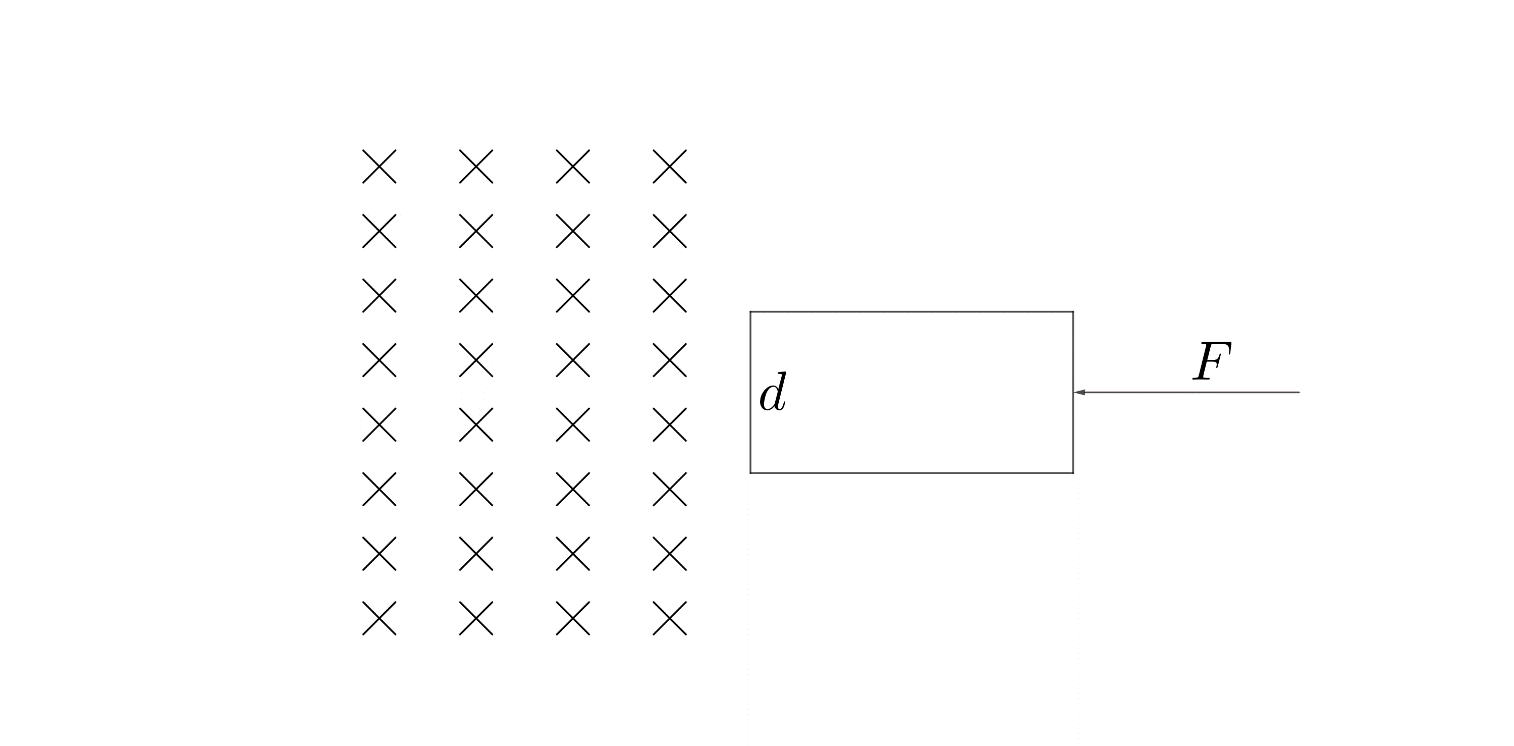
Answer 1

Hint: Acceleration can be found from the net force acting on the wireframe due to the magnetic field and the external force acting on the wireframe travelling through the magnetic field. Terminal velocity can be defined as the velocity by which the loop is moving till the complete loop has entered the magnetic field.

Complete step by step answer:
Let us note down the given data;
The width of the rectangular wire frame = $ d $
The mass of the rectangular wire frame = $ m $
The resistance of the rectangular wire frame = $ R $
Magnitude of uniform magnetic field = $ B $
Magnitude of the force acting on the wireframe = $ F $
Acceleration of the wireframe = $ a $
Velocity of the wireframe = $ v $
(A)
To find the acceleration
We know that as the wireframe moves into the magnetic field, an emf will be induced in the wire perpendicular to the magnetic field and perpendicular to the velocity which is given as,
Induced emf $ \varepsilon =Bdv $
Now, due to this induced emf, a current also flows through the wireframe, which can be expressed from the Ohm’s Law as
 $ I=\dfrac{\varepsilon }{R}=\dfrac{Bdv}{R} $
Now, we know that when a current carrying conductor enters a magnetic field, a force is exerted by the magnetic field in the opposite direction of its motion.
Hence, the force on a current carrying conductor is,
 $ F=IlB $
Substituting the given values,
 $ \therefore F=\left( \dfrac{Bdv}{R} \right)\left( dB \right) $
 $ \therefore F=\dfrac{{{B}^{2}}{{d}^{2}}v}{R} $
Now, this force acts in the opposite direction to the external force acting, hence the resultant force is given as,
 $ {{F}_{net}}=F-\dfrac{{{B}^{2}}{{d}^{2}}v}{R} $
The net force from the Newton’s Second Law of motion can be written as,
 $ \therefore ma=\dfrac{FR-{{B}^{2}}{{d}^{2}}v}{R} $
 $ \therefore a=\dfrac{FR-{{B}^{2}}{{d}^{2}}v}{mR} $
This is the acceleration of the wireframe.
(B)
The terminal velocity $ v_0 $ is the constant value of velocity till the whole wireframe enters the magnetic field. As the velocity is constant, the acceleration is zero.
From the value of acceleration above,
 $ \therefore 0=\dfrac{FR-{{B}^{2}}{{d}^{2}}v}{mR} $
 $ \therefore 0=FR-{{B}^{2}}{{d}^{2}}v $
Replacing velocity with terminal velocity,
 $ \therefore FR={{B}^{2}}{{d}^{2}}{{v}_{0}} $
 $ \therefore {{v}_{0}}=\dfrac{FR}{{{B}^{2}}{{d}^{2}}} $
This is the value of the terminal velocity.
As all the values are constant, we can prove that the value of terminal velocity is constant.
(C)
The value of velocity in terms of $ t $
We know that acceleration is defined as the change in velocity per unit time.
Hence, the value of acceleration is written as,
 $ \therefore \dfrac{dv}{dt}=\dfrac{FR-{{B}^{2}}{{d}^{2}}v}{mR} $
 $ \therefore \dfrac{dv}{FR-{{B}^{2}}{{d}^{2}}v}=\dfrac{dt}{mR} $
Applying integration on both sides for time $ t=0 $ to $ t=t $
 $ \therefore \int\limits_{0}^{v}{\dfrac{dv}{FR-{{B}^{2}}{{d}^{2}}v}}=\int\limits_{0}^{t}{\dfrac{dt}{mR}} $
 $ \therefore \left[ \ln \left( FR-{{B}^{2}}{{d}^{2}}v \right) \right]_{0}^{v}\times \dfrac{1}{-{{B}^{2}}{{d}^{2}}}=\left[ \dfrac{t}{mR} \right]_{0}^{t} $
Substituting the boundary values,
 $ \therefore \left[ \ln \left( FR-{{B}^{2}}{{d}^{2}}v \right)-\ln \left( FR \right) \right]=\left[ \dfrac{-{{B}^{2}}{{d}^{2}}t}{mR} \right] $
 $ \therefore \ln \left( \dfrac{FR-{{B}^{2}}{{d}^{2}}v}{FR} \right)=\dfrac{-{{B}^{2}}{{d}^{2}}t}{mR} $
Changing the logarithmic function to the exponential function,
 $ \therefore \dfrac{FR-{{B}^{2}}{{d}^{2}}v}{FR}={{e}^{\dfrac{-{{B}^{2}}{{d}^{2}}t}{mR}}} $
 $ \therefore 1-\dfrac{{{B}^{2}}{{d}^{2}}v}{FR}={{e}^{\dfrac{-{{B}^{2}}{{d}^{2}}t}{mR}}} $
From the value of terminal velocity we can write,
 $ \dfrac{{{B}^{2}}{{d}^{2}}}{R}=\dfrac{F}{{{v}_{0}}} $
Substituting this value in the equation of velocity,
 $ \therefore 1-\dfrac{v}{{{v}_{0}}}={{e}^{\dfrac{-Ft}{m{{v}_{0}}}}} $
 $ \therefore 1-{{e}^{\dfrac{-Ft}{m{{v}_{0}}}}}=\dfrac{v}{{{v}_{0}}} $
Making velocity the subject of the equation,
 $ \therefore v={{v}_{0}}\left( 1-{{e}^{\dfrac{-Ft}{m{{v}_{0}}}}} \right) $

Note:
For the emf to be induced, the wire should be perpendicular to the field as well as the direction of motion. Hence, the emf will only be induced in the width of the loop. Also from the value of the terminal velocity, we can see that all the terms are constant. Hence, the value of terminal velocity will be constant till the whole loop enters the field.