Question

The rectangular sheet of paper $30cm \times 18cm$ can be formed into the curved surface area of the right circular cylinder in 2 ways. Find the ratio of volumes of two cylinders thus formed.

Answer 1

Hint: One of the sides of the rectangle will be the height of the cylinder and the other side will be the circumference of the circle. We will use the circumference of the circle to find the radius of the cylinder. Then, find the volume of both the cylinders formed, using the formula, $\pi {r^2}h$ , where $r$ is the radius and $h$ is the height of the cylinder. Then, take the ratio of the cylinders.

Complete step-by-step answer:
When we rotate the rectangular sheet keeping the height as 30 cm , then the length of the rectangle will be equal to circumference of the circular face.

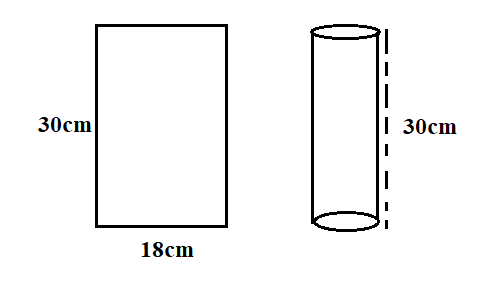
That is
$2\pi {r_1} = 18$
On dividing by $2\pi $, we will get the radius of the cylinder as
${r_1} = \dfrac{{18}}{{2\pi }}$
Then the volume of the cylinder will be $\pi {r_1}^2{h_1}$
On substituting the value of ${r_1}$ and ${h_1}$we will get,
  $\pi {\left( {\dfrac{{18}}{{2\pi }}} \right)^2}\left( {30} \right) = \pi {\left( {\dfrac{9}{\pi }} \right)^2}30$
Next, we will fold the rectangular sheet such that the height of the cylinder formed is 18 cm and then the circumference of the circular face will be 30 cm

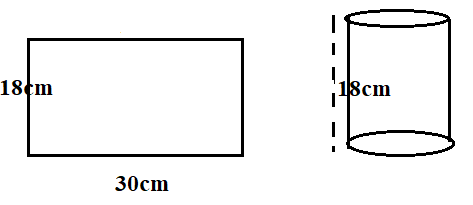
$2\pi {r_2} = 30$
Divide equation by $2\pi $
$ \Rightarrow {r_2} = \dfrac{{30}}{{2\pi }}$
On substituting the value of ${r_2}$ and ${h_2}$ in the volume of the cylinder we will get,
$ \Rightarrow \pi {\left( {\dfrac{{30}}{{2\pi }}} \right)^2}\left( {18} \right) = \pi {\left( {\dfrac{{15}}{\pi }} \right)^2}\left( {18} \right)$
Then the ratio of the volume of the cylinders is
$
   \Rightarrow \dfrac{{\pi {{\left( {\dfrac{9}{\pi }} \right)}^2}\left( {30} \right)}}{{\pi {{\left( {\dfrac{{15}}{\pi }} \right)}^2}\left( {18} \right)}} = \dfrac{{{9^2} \times 15}}{{{{15}^2} \times 9}} \\
   \Rightarrow \dfrac{9}{{15}} \\
   \Rightarrow \dfrac{3}{5} \\
$
Hence the ratio of volumes of cylinder when the cylinder is folded keeping the height as 30 cm to the volume of the cylinder rotated keeping the height as 18 cm is 3:5.


Note: The volume of the cylinder is the space enclosed by the cylinder. Volume of any object is measured in cubic units. When numbers are written ratio, the order plays an important role, the statement written first corresponds to the first number in the ratio.