Question

The rear side of the truck is open and a box of mass 50kg is placed at 3.2m away from the open end. The coefficient of friction between the box and the surface is 0.2. If the truck starts from rest and moves on a straight road with acceleration$2.1m{{s}^{-2}}$, the box falls off the truck after a time. $\left( g=10m{{s}^{-2}} \right)$
A. $\dfrac{8}{\sqrt{41}}s$
B. $4s$
C. $8s$
D. $\sqrt{8}s$

Answer 1

Hint: As a first step, you could make a free body diagram and thus balance the forces acting in the opposite direction. Then you could consider the relative motion between the box and the truck. After finding the relative acceleration, you could substitute it along with other given quantities in the equation of motion to find the time.
Formula used:
Equation of motion,
${{s}_{BT}}={{u}_{BT}}t+\dfrac{1}{2}{{a}_{BT}}{{t}^{2}}$

Complete step by step answer:
In the question, we are given a truck and its one side is open and at 3.2m away from this open end a mass 50kg is kept. The coefficient of friction between the box and surface is given to be 0.2. The box is seen to fall off after certain time t when this truck starts from rest and accelerates on a straight road with acceleration$2.1m{{s}^{-2}}$. We are supposed to find this time t.

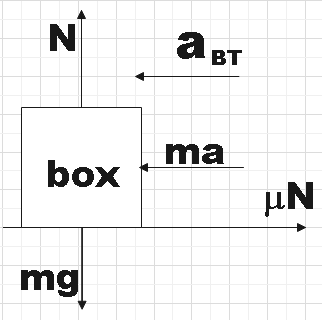
From the free body diagram above we have,
$N=mg$
Now, we could give the motion of the box with respect to the truck as,
$ma-\mu N=m{{a}_{BT}}$
$\Rightarrow ma-\mu mg=m{{a}_{BT}}$
${{a}_{BT}}=2.1-\left( 0.2 \right)\left( 10 \right)=0.1m{{s}^{-2}}$ ……………………………………………. (1)
Now, we have the equation of motion,
${{s}_{BT}}={{u}_{BT}}t+\dfrac{1}{2}{{a}_{BT}}{{t}^{2}}$
Substituting the given values and also (1),
$3.2=0+\dfrac{1}{2}\left( 0.1 \right){{t}^{2}}$
$\Rightarrow {{t}^{2}}=64$
$\therefore t=8s$
Therefore, we found the time taken by the box to fall off the truck to be 8s.
So, the correct answer is “Option C”.

Note: In the question, we are given that the distance between the open end and the box is 3.2m. So, we could make this conclusion that the box will have to travel that distance so as to fall off from the truck. Thus, we have substituted this for the displacement in the equation of motion and thus found the answer.