Question

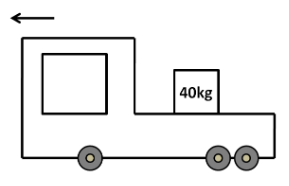
The rear side of a truck is open and a box of $ 40kg $ mass is placed $ 5m $ away from the open end as shown in the figure. The coefficient of friction between the box and the surface below it is $ 0.15 $ . On a straight road, the truck starts from rest and accelerates with $ 2m{s^{ - 2}} $ . Find the distance (in $ {\text{m}} $ ) travelled by truck by the time the box falls from the truck. (Ignore the size of the block)

Answer 1

Hint : To solve this question, we need to find out the acceleration of the block with respect to the truck by applying the concept of pseudo force. Then using the second equation of motion we can find out the time when the box falls from the truck. Finally, using the same equation of motion we can find out the distance travelled by the truck by this time.

Formula used: The formula used to solve this question is given by
 $ s = ut + \dfrac{1}{2}a{t^2} $ , here $ s $ is the displacement, $ u $ is the initial velocity, $ a $ is the acceleration, and $ t $ is the time.

Complete step by step answer:
When the truck is accelerating towards the left, a pseudo force will act on the box towards the right in the frame of reference of the truck. Also since the surface of the truck is rough, frictional force will act on the box towards the left. So the free body diagram of the box is as shown below.
Let $ A $ be the acceleration of the box.
As there is no vertical motion of the box, so we have
 $ N = 40g $ (1)
Now, the net force on the block is
 $ 40a - f = 40A $
The force due to friction is given as, $ f = \mu N $ . So we have
 $ 40a - \mu N = 40A $
From (1)
 $ 40a - 40\mu g = 40A $
Dividing by $ 40 $ both the sides, we get
 $ a - \mu g = A $
 $ \Rightarrow A = a - \mu g $
According to the question, $ a = 2m{s^{ - 2}} $ , $ \mu = 0.15 $ . Also we know that $ g = 10m/{s^2} $ . Substituting these above we get
 $ A = 2 - 0.15 \times 10 $
 $ \Rightarrow A = 0.5m/{s^2} $
So the acceleration of the box is $ 0.5m/{s^2} $ towards the right.
Now, let $ t $ be the time when the box falls from the truck. Since the box is placed at a distance of $ 5m $ away from the open end, so the displacement of the box till time $ t $ is equal to $ 5m $ . From the second equation of motion we have
 $ s = ut + \dfrac{1}{2}a{t^2} $
Since the truck is starting from rest, the block will also start from rest giving $ u = 0 $ . This implies
 $ s = \dfrac{1}{2}a{t^2} $
Substituting $ s = 5m $ , $ a = A = 0.5m/{s^2} $ , we get
 $ 5 = \dfrac{1}{2} \times 0.5 \times {t^2} $
 $ {t^2} = 20 $
Taking square root both the sides, we get
 $ t = \sqrt {20} s $
 $ \Rightarrow t = 2\sqrt 5 s $ (2)
Now, let the distance travelled by the truck by this time be $ d $ . Substituting this in the second equation of motion, we get
 $ d = ut + \dfrac{1}{2}a{t^2} $
The truck starts from rest, therefore $ u = 0 $ .
 $ d = \dfrac{1}{2}a{t^2} $
The acceleration of the truck is $ a = 2m{s^{ - 2}} $ . Also, from (2) $ t = 2\sqrt 5 s $ , which gives
 $ d = \dfrac{1}{2} \times 2 \times {\left( {2\sqrt 5 } \right)^2} $
 $ \Rightarrow d = 20m $
Hence the distance travelled by the truck by the time box falls from the truck is equal to $ 20m $ .

Note:
We need to look for the tendency of motion of the box with respect to the surface of the truck to check the direction of friction acting on the box. As the friction opposes the relative motion between two surfaces, so the friction will oppose the tendency of motion of the block.