Question

The ratio of measure of the consecutive angles of a quadrilateral is 1:2:3:4. What type of quadrilateral is it?\[\]
(a) Kite\[\]
(b) Parallelogram\[\]
(c) Trapezium\[\]
(d) Square.\[\]

Answer 1

Hint: We assume the first angle has measurement $x=A$ in degree in the quadrilateral ABCD. So the other angle will be $B=2x,C=3x,D=4x$. We use the facts that the sum of all angles in a quadrilateral is ${{360}^{\circ }}$ and the two lines are parallel when the sum of the angles made by a line intersecting both of them at one side is ${{180}^{\circ }}$.\[\]

Complete step-by-step answer:
Let us try to remember the definitions of all the figures mentioned one by one. First let us start with parallelograms. So, a parallelogram is a quadrilateral in which each pair of opposite angles are equal. \[\]
 

If we talk about kite, it is a quadrilateral with one pair of opposite sides equal and diagonals are perpendicular to each other.\[\]
 

Now, a rectangle is a parallelogram with each of the interior angles measuring $90{}^\circ $while squares are the parallelograms with all the properties of a rectangle along with the constraint that all its sides must be equal.\[\]
 

Finally, a trapezium is a quadrilateral with one pair of opposite sides parallel and another pair of opposite sides is non-parallel. For a trapezium there is no constraint that two of the angles are equal.\[\]
 

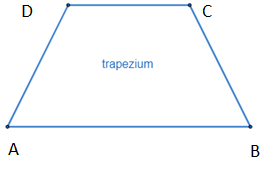
We are given that the ratio of measure of the consecutive angles of a quadrilateral say ABCD is 1:2:3:4. Let us assume the first angle has measurement $x=A$ in degree. So the other angle will be $B=2x,C=3x,D=4x$. We know that the sum of the angles in a quadrilateral is ${{360}^{\circ }}$. So we have
\[\begin{align}
  & x+2x+3x+4x={{360}^{\circ }} \\
 & \Rightarrow 10x={{360}^{\circ }} \\
 & \Rightarrow x={{36}^{\circ }} \\
\end{align}\]
So the measure of the angles are $A=x={{36}^{\circ }},B=2x={{72}^{\circ }},C=3x={{108}^{\circ }},D=4x={{144}^{\circ }}$. We know that two lines are parallel when the sum of the angles made by a line intersecting both of them at one side is ${{180}^{\circ }}$. We see here that
\[\begin{align}
  & A+D={{36}^{\circ }}+{{144}^{\circ }}={{180}^{\circ }} \\
 & B+C={{72}^{\circ }}+{{108}^{\circ }}={{180}^{\circ }} \\
\end{align}\]
We denote the angles A,D and B,C are adjacent angles. So in the quadrilateral AD is the line that cuts parallel lines CD and AB. Similarly BC cuts parallel the same lines CD and AB. So we have only one pair of parallel sides CD and AB opposite to each other. So the given quadrilateral ABCD is a trapezium. \[\]

Note: We note that if we would have found another two pairs of angles say A and B , C and D whose sum is ${{180}^{\circ }}$, the quadrilateral ABCD would have been a parallelogram. The consecutive sides of a kite , parallelogram and square are respectively in the ratio $a:b:b:a,a:b:a:b,1:1:1:1$ where $a,b$ are real numbers.