Question

The range of a rifle bullet is 1000m, when \[\theta \] is the angle of projection. If the bullet is fired with the same angle of projection from a car travelling horizontally at \[36km/hr\] towards the target, the increase in the range will be:
(given \[\sqrt{\dfrac{5}{9.8}}=0.712\])
(a) \[173\sqrt{\tan \theta }\]
(b) \[183\sqrt{\tan \theta }\]
(c) \[143\sqrt{\tan \theta }\]
(d) \[113\sqrt{\tan \theta }\]

Answer 1

Hint: For this question, we need to remember the formula of horizontal distance/range and velocity of car is mentioned in the question. The vertical and horizontal components play a crucial role in the given solution.
Formula used:
Range\[R=\dfrac{2{{u}^{2}}\sin \theta \cos \theta }{g}\]

Complete answer:
Let us consider a bullet projected at an angle \[\theta \] and the maximum distance covered i.e. range is 1000m. Now, according to the question if the same bullet will be fired with the same angle of projection, when travelling from a car moving with the velocity \[36km/hr\], we need to find the range.

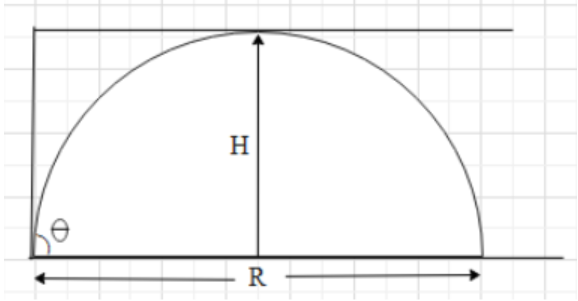
Given data -
                          velocity(u)= \[36km/hr=10m/s\]
Initial range \[R=\dfrac{2{{u}^{2}}\sin \theta \cos \theta }{g}\]
                      \[R=\dfrac{2}{g}PQ\]…………(1)
Here \[P=u\cos \theta ,Q=u\sin \theta \]
let range be \[{{R}^{'}}\] when the bullet is projected from a car.
\[{{R}^{'}}=\dfrac{2}{g}(P+10)Q\]………(2)
As the range is changing, therefore the vertical component will remain the same.

Difference in range \[{{R}^{'}}-R=\dfrac{20Q}{g}=\dfrac{20u\sin \theta }{g}\]

From (1) \[R=\dfrac{2{{u}^{2}}\sin \theta \cos \theta }{g}=1000\]

Rearranging the terms, \[{{u}^{2}}=\dfrac{1000\times g}{2\sin \theta \cos \theta }\]

Solving (1) and (2) \[R-{{R}^{'}}=\dfrac{20\sqrt{1000}}{5g}\times \dfrac{\sqrt{\tan \theta }}{\sqrt{2}}\]
                                             \[=143\sqrt{\tan \theta }\]
Therefore, the difference in range is found to be \[143\sqrt{\tan \theta }\] .

So option C is the correct answer.

Additional Information:
Range of an object is the maximum horizontal distance the object can cover when projected at any angle. Solving these kinds of problems, we have to be careful while breaking the vector into its component, i.e. horizontal component along x – axis and vertical component along y-axis.

Note:
It is better to draw face body drawing which will help to break the vector into its component. Face body diagram helps in visualizing the scenario framed in the question. The formula for height and range is alike, so it should not be confused.