Question

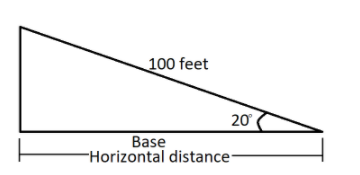
The ramp must be exactly 100 feet in length and make a \[{{20}^{\circ }}\] angle with the level ground. What is the horizontal distance, in meters, from the start of the ramp to the point level of the ramp immediately below the entrance of the mall, rounded to the nearest metre?

Answer 1

Hint: The first thing we need to understand in this question is that there is formation of a right angle triangle in which the base of the triangle is the horizontal distance from the ground level point of ramp till the starting point of mall measured on the ground level too and the perpendicular is the height of mall from the ground level and at the end the hypotenuse is the length of ramp. We are given with the angle made by the ramp with the ground, which is \[{{20}^{\circ }}\], with the help of which we will calculate the horizontal distance by taking the cosine of that angle which is \[\cos \theta =\dfrac{base}{hypotenuse}\].

Complete step-by-step answer:
Now in this question there is a ramp inclined at \[{{20}^{\circ }}\] angle with the ground level and we need to find the horizontal distance from the point of ramp in contact with the ground and the point on the ground directly below the finishing point of ramp or starting point of mall.

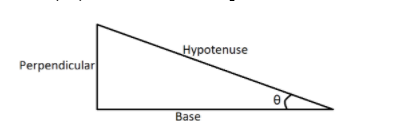
As we can see that there is formation of a right angle triangle in which the ramp is the hypotenuse, the horizontal distance is the base of the triangle and the height of the mall entrance from the ground level is the perpendicular of the triangle.

Now in the question we are given with the length of the ramp which is the hypotenuse of the triangle and the angle the ramp makes with the level ground or the base of the triangle, which is \[{{20}^{\circ }}\], and we have to find the horizontal distance or the length of base of the right angle triangle.
Now as we know the length of hypotenuse and we want to find the length of the base of the triangle, we are also given the angle between them, so we will use the trigonometric function \[cosine\theta \] or \[cos\theta \].
\[\cos \theta \] is represented in the form of ratio between base of the triangle to the hypotenuse of the triangle, mathematically represented as,

\[\cos \theta =\dfrac{base}{hypotenuse}\]
Putting the values we know in the above equation, we get,
\[\cos {{20}^{\circ }}=\dfrac{base}{100}\]
\[base=\cos {{20}^{\circ }}\times 100\]
\[base=0.9397\times 100=93.97feet\]
Hence the value of base is 93.97 feet but we want to find its value in meters and also round off it to nearest natural number.
Now we need to remember the conversion values like,
\[2.54cm=1inch\] and,
\[1foot=12inches\]
\[1foot=12inches=12\times 2.54cm.=30.48cm.\]
So \[93.97feet\] when converted into centimeters will be,
\[93.97feet=93.97\times 30.48cm=2864.2056cm.\]
If we want to convert centimeters to meters we need to divide it by 100
So \[93.97feet\] when converted into meters will be,
\[93.97feet=\dfrac{2864.2056}{100}m=28.64m\]
When we round off to nearest number, we get,
\[93.97feet=29m\]
Hence the final answer is \[29m\].

Note: Always remember that these trigonometric functions like \[\sin \theta {{,}_{{}}}\cos {{\theta }_{{}}},\tan {{\theta }_{{}}},\sec {{\theta }_{{}}},\operatorname{cosec}{{\theta }_{{}}},\cot \theta \] are always used in the right angled triangles. The maximum and minimum value of \[\cos \theta \] function is \[{{1}_{{}}} an{{d}_{{}}}-1\]. We can also solve this question by using an alternative method which is \[\sec \theta =\dfrac{hypotenuse}{base}\] as \[\cos \theta =\dfrac{1}{\sec \theta }\]. The values of some angles of these trigonometric functions are needed to be remembered but the one used in this question will be given to you in the exam. Also remember the conversion relations only the important ones like feet to metre inches to centimetres and so on. If one was asked about other terms then follow the table below.