Question

The radius of the outer circumference of a cylindrical ring is $ 12 $ cm and the diameter of the cross-section is $ 1.5 $ cm. Then, the volume of circular ring is

Answer 1

Hint: Here first of all we will convert the given radius in the form of the diameter and then will place its area to get the area of the outer surface of the ring and similarly will find the area for the cross-section and then will find its volume by using the values of area and the third measure.

Complete step by step solution:

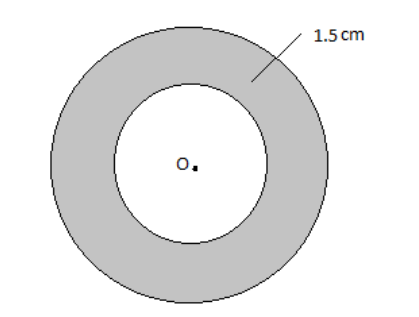
Given that the radius of the outer circumference of a cylindrical ring is $ 12 $ cm
Let the diameter of the cylindrical be “D”
 $ D = 2(12) = 24cm $ (Since diameter is double of the radius)
Also, given that the diameter of the cross – section is $ d = 1.5cm $
Now, the area of the cross – section can be given by –
 $ A = \dfrac{\pi }{4}{(1.5)^2} $
Simplify the above expression finding the product and division of the terms –
 $ A = 1.76625c{m^2} $ ….. (A)
Also, the volume of the circular ring is given by the product of the area and the measure of third side.
Volume of the circular ring, $ V = AI $
Where, $ I = \pi (D - d) $
Place the values in the above expression –
 $ I = \pi (24 - 1.5) $
Simplify the above expression finding the difference and then the product of the terms –
 $ I = 3.14(22.5) $
Simplify the above terms –
 $ I = 70.65 $ cm ….. (B)
Now, the volume of the circular ring is given by –
 $ V = 1.76625 \times 70.65 $
Simplify the above expression –
 $ V = 124.785c{m^3} $
The above value can be re-written as –
 $ V = 125c{m^3} $
Thus, the volume of the circular ring is $ 125c{m^3} $
So, the correct answer is “ $ 125c{m^3} $ ”.

Note: Always put the correct units at the end of the solutions after the values are calculated. Always remember that perimeter is measured in meters or centimetres, area in square units and the volume is measured in cubic units. Area of the circular ring can be calculated by two formulas based on radius and diameter. Radius is half of the diameter.