Question

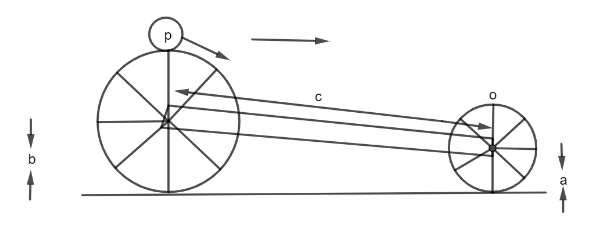
The radius of the front wheel of the arrangement shown in figure is \[a\] and that of the rear wheel is \[b\] . If a dust particle driven from a highest point of rear wheel alights on the highest point of front wheel, the velocity of arrangement is:

A. ${\left[ {g\dfrac{{\left( {b - a} \right)\left( {c - a + b} \right)}}{{c + a - b}}} \right]^{\dfrac{1}{2}}}$
B. $\dfrac{{g(c + a + b)}}{{4\left( {b - a} \right)}}$
C. ${\left[ {g\dfrac{{(c + a - b)\left( {c - a + b} \right)}}{{4\left( {b - a} \right)}}} \right]^{\dfrac{1}{2}}}$
D. ${\left[ {\dfrac{{g\left( {c - a + b} \right)}}{{4\left( {c - a} \right)}}} \right]^{\dfrac{1}{2}}}$

Answer 1

Hint: In order to solve this problem first we will find the horizontal distance between their centers, after that we will find the horizontal distance travelled by the wheel in time t. Then we will equate both the equations in order to find the value of the term t and at last we will substitute the value of t inorder to get the required velocity of arrangement.

Complete step by step answer:
Let $t$ be time of flight of the particle from P to Q .Since C is the distance between the centres of the two wheels,
${c_h} = \sqrt {{c^2} - {{\left( {b - a} \right)}^2}} $
If $v$ is the velocity of the carriage, then ${c_h} = vt$ (horizontal range).
$vt = \sqrt {{c^2} - {{\left( {b - a} \right)}^2}} $
$\Rightarrow t = \dfrac{1}{v}\sqrt {{c^2} - {{\left( {b - a} \right)}^2}} $

In this time, the particle has covered the vertical distance $ = 2b - 2a$.
(The vertical distance between the highest points of both the wheels)
\[2b - 2a = \dfrac{1}{2}g{t^2} \\
\Rightarrow 2\left( {b - a} \right) = \dfrac{1}{2}g\dfrac{{\left[ {{c^2} - {{\left( {b - a} \right)}^2}} \right]}}{{{v^2}}} \\
\Rightarrow {v^2} = \dfrac{g}{4}\dfrac{{{c^2} - {{\left( {b - a} \right)}^2}}}{{\left( {b - a} \right)}} \\
\therefore v = {\left[ {g\dfrac{{\left( {c + a - b} \right)\left( {c - a + b} \right)}}{{4\left( {b - a} \right)}}} \right]^{\dfrac{1}{2}}} \]
Therefore, the velocity of the arrangement is \[{\left[ {g\dfrac{{\left( {c + a - b} \right)\left( {c - a + b} \right)}}{{4\left( {b - a} \right)}}} \right]^{\dfrac{1}{2}}}\].

So, the correct option is C.

Note: While solving these type questions one must take care of the direction of acceleration of the arrangement. Here in this only vertical acceleration is present, in vertical direction there is no acceleration component. Since there was no external force acting on the arrangement except gravity we have used this method.