Question

The radius of the circle of sphere ${x^2} + {y^2} + {z^2} = 49$ and plane $2x + 3y - z - 5\sqrt {14} = 0$ is
A. $\sqrt 6 $
B. $2\sqrt 6 $
C. $4\sqrt 6 $
D. None of these

Answer 1

Hint: First we will write the general equation of a sphere i.e. ${\left( {x - l} \right)^2} + {\left( {y - m} \right)^2} + {\left( {z - n} \right)^2} = {r^2}$ , now we will compare it with the given equation of sphere to get the coordinate of centre and the radius of the circle, using this we’ll find the distance of the circle from the centre of the sphere as we know the circle also lie on the plane mentioned and will assume a point at the circumference of the circle. Now we using this point and the center of the circle and the centre of the sphere, as they will form a right triangle, we’ll use the Pythagoras theorem which states that in a right triangle ABC right-angled at A then the sum of the square of perpendicular and base is equal to the square of hypotenuse i.e. $B{C^2} = A{B^2} + C{A^2}$, hence will find the measurement of the radius.

Complete step by step answer:

Given data: ${x^2} + {y^2} + {z^2} = 49$
$2x + 3y - z - 5\sqrt {14} = 0$

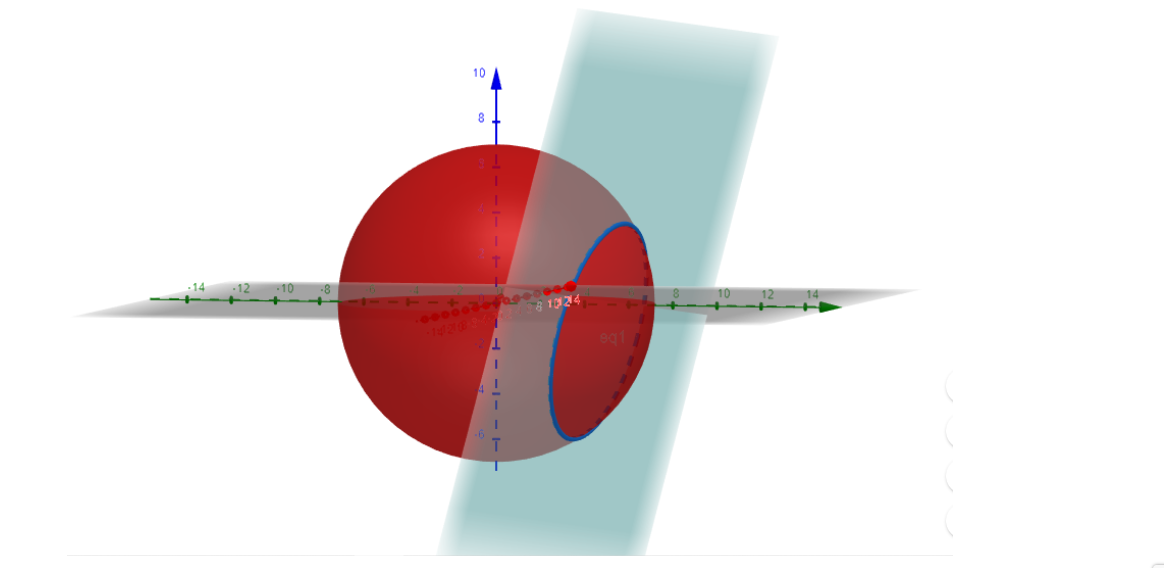
If the equation of the sphere is ${\left( {x - l} \right)^2} + {\left( {y - m} \right)^2} + {\left( {z - n} \right)^2} = {r^2}$ ,
Then the centre of the sphere is $(l,m,n)$ and r is the radius
On comparing this with the given equation of sphere i.e. ${\left( {x - 0} \right)^2} + {\left( {y - 0} \right)^2} + {\left( {z - 0} \right)^2} = 49$
Therefore the centre of the sphere let say O is $(0,0,0)$ and radius $ = 7$
Now, let the centre of the circle required be ‘A’ and a point anywhere in the circumference be ‘B’

We know that the distance of any point $P(p,q,r)$ from the plane $ax + by + cz + d = 0$ is given by
 $ = \dfrac{{\left| {ap + bq + cr + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$
Since the circle is the intersection of sphere and plane, we can say that A and B are on the given plane where OA is perpendicular to the plane
 $\therefore OA = \dfrac{{\left| {2(0) + 3(0) - (0) - 5\sqrt {14} } \right|}}{{\sqrt {{2^2} + {3^2} + {{( - 1)}^2}} }}$
On simplification we get,
 $ = \dfrac{{5\sqrt {14} }}{{\sqrt {4 + 9 + 1} }}$
On solving denominator, we get,
 $ = \dfrac{{5\sqrt {14} }}{{\sqrt {14} }}$
On cancelling common terms, we get,
  $ = 5$
We know that if in a right triangle ABC right angled at A, then Pythagoras theorem states that
 $B{C^2} = A{B^2} + C{A^2}$
Then using Pythagoras theorem in triangle OAB right-angles at A
 $ \Rightarrow O{B^2} = O{A^2} + A{B^2}$
Substituting the value of OA and OB as OB is the radius of the sphere
 $ \Rightarrow {7^2} = {5^2} + A{B^2}$
On squaring and rearranging we get,
 $ \Rightarrow 49 - 25 = A{B^2}$
On simplification we get,
 $ \Rightarrow A{B^2} = 24$
On taking the positive square root, we get,
 $ \Rightarrow AB = \sqrt {24} $
 $ \Rightarrow AB = 2\sqrt 6 $
From the above figure, we can say that AB is the radius of the required circle
Option(B) is correct.

Note: Most of the students use the distance formula of a point let say $P(p,q,r)$ from the plane $ax + by + cz + d = 0$ as $\dfrac{{\left| {ap + bq + cr} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$ they put the constant term in the right-hand side so avoid doing that as the correct formula for the distance is given by $\dfrac{{\left| {ap + bq + cr + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$ .
As we mentioned the general equation of the sphere is ${\left( {x - l} \right)^2} + {\left( {y - m} \right)^2} + {\left( {z - n} \right)^2} = {r^2}$ , do not get confuse it with the general equation of the circle in 3D, as the equation of the circle in 3D is also given by ${\left( {x - l} \right)^2} + {\left( {y - m} \right)^2} + {\left( {z - n} \right)^2} = {r^2}$ , as we have given that the equation is of a sphere so we will not confuse our self it with the equation of a circle.