Question

The radius of the circle is $17cm$ and the length of one of its chord is $16cm$. Find the distances of the chord from the centre.

Answer 1

Hint: We know the perpendicular drawn from the center divide the chord. We need to know the theorem of circle which says that when a line is drawn from the centre of circle perpendicular to the chord then it divides the chord into two equal parts. Also, we need to know about Pythagoras theorem of right-angle triangles.

Complete step by step solution:
Let there be a circle with centre \[\left( O \right)\] and radius \[\left( {OA} \right)\] and let there be a chord \[\left( {AB} \right)\] inside the circle on which a perpendicular \[\left( {OX} \right)\] from the centre of the circle is made.
                                                  

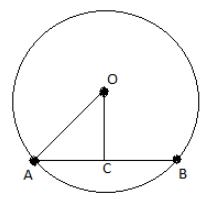
Let $AB$ be the chord with length $ = 16cm$
$OA = radius = 17cm$
Now, OC is perpendicular to AB.
$Then\;AC = CB = 8cm = \dfrac{{AB}}{2}$

$[\because \,$Perpendicular drawn from the center to the chord, bisect the chord$]$
By using by Pythagoras theorem in $\triangle OAC$
$O{A^2} = O{C^2} + A{C^2}$
$O{C^2} = O{A^2} - A{C^{^2}}$
$OC = \sqrt {{{17}^2} - {8^2}}$
$\Rightarrow\sqrt {289 - 64}$
$\Rightarrow\sqrt {225}$
$\therefore OC = 15cm$

Thus, the correct answer is $OC = 15cm$.

Note: Perpendicular drawn from centre to any chord divide the chord into two equal parts and equal chords are equidistant from the centre. We should have knowledge about the formula of Pythagoras theorem for a right triangle $ABC$ that can be represented as $A{B^2} + B{C^2} = A{C^2}$.