Question

The radius of the base of a right cylinder is halved, keeping the height the same, then find the ratio of the volume of the cylinder thus obtained to the volume of the original cylinder.

Answer 1

Hint: Now we know that the volume of the cylinder is given by $\pi {{r}^{2}}h$. Hence we first find the volume of the original cylinder. Then for the new cylinder, we know that the radius of the base is halved, so we take a new radius as half of the original one. Also, it is given that the height remains the same hence we take height equal to the original one. Now with these new measurements again calculate the Volume of the cylinder. Now once we have the volume of the new cylinder and the volume of an original cylinder we will take its ratio.

Complete step-by-step solution:
Now let us consider the original cylinder. Let ${{r}_{1}}$ be the radius of the original cylinder and h be the height of the original cylinder

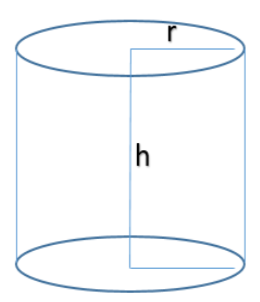
Now we know that the Volume of the cylinder is given by $\pi {{r}^{2}}h$ where r is the radius of the base and ‘h’ is the height of the cylinder.
Now let the Volume of the original cylinder be ${{V}_{1}}$. hence by applying the above formula we get
${{V}_{1}}=\pi {{r}_{1}}^{2}h............(1)$
Now Consider the new Cylinder since the radius is halved radius of the base of the new cylinder becomes $\dfrac{{{r}_{1}}}{2}$ and the height of the new cylinder remains the same hence h

Let ${{V}_{2}}$ be the volume of new cylinder
Hence we get
\[\begin{align}
  & {{V}_{2}}=\pi {{\left( \dfrac{{{r}_{1}}}{2} \right)}^{2}}h \\
 & =\pi \left( \dfrac{{{r}_{1}}^{2}}{4} \right)h \\
 & =\dfrac{\pi {{r}_{1}}^{2}h}{4} \\
\end{align}\]
Now from equation (1) we get ${{V}_{2}}=\dfrac{{{V}_{1}}}{4}$
Hence ${{V}_{2}}:{{V}_{1}}=1:4$
Hence we get the required ratio is $1:4$

Note: Now note that here radius is just halved but the Volume changes by $\dfrac{1}{4}$ and not $\dfrac{1}{2}$. Hence do not make a mistake by considering the volume is also halved. To find the correct ratio substitute the value according to the condition in the formula.
Now we can also do this with a shortcut trick. Since we know that only radius is changing just focus on how Volume varies to radius since Volume depends on radius square $\dfrac{1}{2}$ change in radius will change the volume by ${{\left( \dfrac{1}{2} \right)}^{2}}=\dfrac{1}{4}$