Question

The radius of the base of a right circular cone of a semi-vertical angle $\alpha $ is r. Show that its volume is $\dfrac{1}{3}\pi {{r}^{3}}\cot \alpha $ and the curved surface area is $\pi {{r}^{2}}\cos ec\alpha $ .

Answer 1

Hint: Use the regular formulas of volume and curved surface area of the cone. Get the relation between the height of the cone, radius and slant height using $\alpha $ .

Complete step-by-step answer:
Before starting the question, it is preferred to have a 2-D, representative diagram of a cone with all the mentioned configurations.
Let’s start by drawing the representative figure according to the data given question:

 

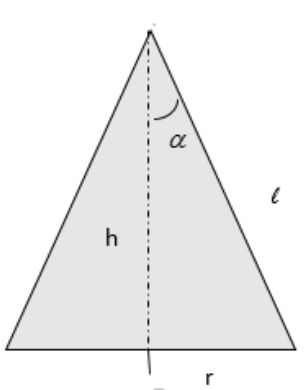
Using the definition of trigonometric ratios for a right-angled triangle:
$\text{sin }\!\!\alpha\!\!\text{ =}\dfrac{\text{perpendicular}}{\text{hypotenuse}}\text{=}\dfrac{\text{r}}{\text{l}}$
\[\Rightarrow l=\dfrac{r}{sin\alpha }\]
And, $\dfrac{1}{\sin \alpha }=\cos ec\alpha $
$\therefore l=r\cos ec\alpha .............(i)$
$\text{cot }\!\!\alpha\!\!\text{ =}\dfrac{base}{perpendicular}\text{=}\dfrac{h}{r}$
\[\therefore h=r\cot \alpha ............(ii)\]
Now, the volume of a cone = $\dfrac{1}{3}\pi {{r}^{2}}h$ .
Substituting the value of h from equation (ii):
Volume of a cone = $\dfrac{1}{3}\pi {{r}^{2}}r\cot \alpha $ .
$\Rightarrow $ Volume of a cone = $\dfrac{1}{3}\pi {{r}^{3}}\cot \alpha $ .
Curved surface area of cone = $\pi rl$ .
Substituting the value of l from equation (i):
Curved surface area of cone = $\pi r\times r\cos ec\alpha $ .
$\Rightarrow $ Curved surface area of cone = $\pi {{r}^{2}}\cos ec\alpha $ .
Hence, we have proved that the curved surface area and the volume of a cone whose base radius is r and semi-vertical angle $\alpha $ are $\pi {{r}^{2}}\cos ec\alpha $ and $\dfrac{1}{3}\pi {{r}^{2}}r\cot \alpha $ respectively.

Note: The vertical angle of the cone is also termed as the Apex angle of the cone. The total surface area of the cone is the sum of the curved surface area and the area of the circle at the base of the cone. A relation to remember between a cone and a cylinder of the same radius and the same height is that the volume of the cone is one-third of the volume of the cylinder.
Other trigonometric ratios are:
$\tan \alpha \text{ },\cos \alpha \text{ },\text{ sec}\alpha .$