Question

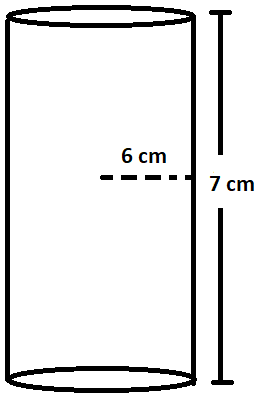
The radius of the base of a right circular cylinder is 6 cm and the height is 7 cm. Find the volume of this cylinder.

Answer 1

Hint: In surface area and volume, we have a formula that can be used to find the volume of a cylinder. For a right circular cylinder having the base radius equal to 6 cm and the height equal to 7 cm, the volume is given by $V=\pi {{r}^{2}}h$. Using this formula, we can solve this question.

Complete step-by-step answer:
Before proceeding with the question, we must know all the formulas that will be required to solve this question.
In surface area and volume, we have a formula that can be used to find the volume of the right circular cylinder having it’s base radius equal to r and it’s height equal to h. The volume of this cylinder is equal to,
$V=\pi {{r}^{2}}h............\left( 1 \right)$
In the question, we are given a right circular cylinder having base radius equal to 6 cm and height equal to 7 cm. Using formula $\left( 1 \right)$, it’s volume is equal to,

$\begin{align}
  & V=\pi {{\left( 6 \right)}^{2}}\left( 7 \right) \\
 & \Rightarrow V=\pi \times 36\times 7 \\
\end{align}$
Since $\pi =\dfrac{22}{7}$, we get,
$\begin{align}
  & V=\dfrac{22}{7}\times 36\times 7 \\
 & \Rightarrow V=792c{{m}^{3}} \\
\end{align}$
Hence the volume of the right circular cylinder is equal to 792 $c{{m}^{3}}$.

Note: There is a possibility that one may commit a mistake while applying the formula to calculate the volume of the cylinder and one may use the value of $\pi$=3.14 which will lead us to an incorrect answer.