Question

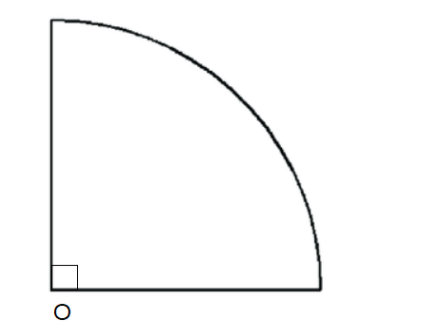
The radius of a circle is 21 cm. find the perimeter and the area of a quadrant of the circle.

Answer 1

Hint: We first find the relation between the whole circle and the quadrant of the circle for perimeter and the area. We find the perimeter and the area of the whole circle and find $ \dfrac{1}{4} $ of those values to find the perimeter and the area of a quadrant of the circle.

Complete step-by-step answer:
The radius of a circle is 21 cm. We need to find the perimeter and the area of a quadrant of that circle.
We know that the ratio of the perimeter and the area of a quadrant will be also $ \dfrac{1}{4} $ of the perimeter and the area of the whole circle. This is dependent on the centre angle ratio. The whole centre angle for the circle is $ {{360}^{\circ }} $ . For the quadrant of the circle, the angle will be $ {{360}^{\circ }}\times \dfrac{1}{4}={{90}^{\circ }} $ .
Following the same ratio then the perimeter and the area of the whole circle get divided by 4.
We know that for a circle of radius $ r $ , the perimeter and the area of the circle will be $ 2\pi r $ and $ \pi {{r}^{2}} $ respectively.
For the given circle of radius 21, the perimeter and the area of the circle will be $ 2\pi \times 21=42\times \dfrac{22}{7}=132 $ cm and \[\pi {{r}^{2}}=\dfrac{22}{7}\times {{21}^{2}}=1386\] square cm respectively.
The perimeter and the area of quadrant of the circle will be $ 132\times \dfrac{1}{4}=33 $ cm and \[\dfrac{1}{4}\times 1386=346.5\] square cm respectively.

Note: Quadrant refers to the four quarters in the coordinate system. Each of the four sections is called a quadrant. When it comes to circles, the quarter of a circle is called a quadrant, which is a sector of $ {{90}^{\circ }} $ . When four such quadrants are joined, the structure that we get is nothing but a circle.