Question

The radius of a circle inscribed in an equilateral triangle is $2$? What is the perimeter of the triangle?

Answer 1

Hint: In this question, first we will find the length of altitude or median of the triangle. We know that any median is divided by a point of intersection with other medians in proportion 1:2. Then we can find the side length of the triangle using trigonometric ratios. Then we can find the perimeter of the triangle by adding all the sides.

Complete step by step answer:

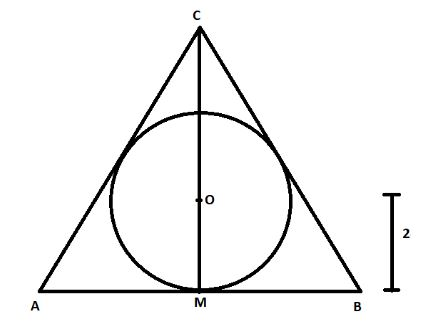
In the above question, it is given that the radius of the circle is $2$and the given triangle is an equilateral triangle. We know that the tangent and the radius to a circle intersect at an angle of ${90^ \circ }$. Therefore, we can say that OM is perpendicular to AB and CM is the altitude. We also know that the measure of angle ACM and angle BCM are equal to $30$ degrees. Therefore, now we can say that triangle ACM is congruent to triangle BCM by side angle side property. So, we can say that $AM = BM$ or we can say that $AM = \dfrac{{AB}}{2}$.

We also know that CM is divided by the point O in the ratio $2:1$ as we know that CM is a median and any median is divided by a point of intersection with other medians in proportion \[1:2\]. Therefore, if the length of OM is $2$, then the length of OC will be $2 \times 2 = 4$. Hence, the length of CM will be $2 + 4 = 6$. Now,let the length of the side of the triangle is $x$. Therefore, the length of AM will be $\dfrac{x}{2}$.Now, we will apply Pythagoras theorem in triangle ACM.Now,
$A{C^2} = A{M^2} + C{M^2}$
Now we will substitute the appropriate values in the above equation.
$ \Rightarrow {\left( x \right)^2} = {\left( {\dfrac{x}{2}} \right)^2} + {\left( 6 \right)^2}$
On transposing, we get
\[ \Rightarrow {x^2} - \dfrac{{{x^2}}}{4} = 36\]

Now, take LCM in left hand side
\[ \Rightarrow \dfrac{{4{x^2} - {x^2}}}{4} = 36\]
\[ \Rightarrow \dfrac{{3{x^2}}}{4} = 36\]
On simplification, we get
\[ \Rightarrow {x^2} = 48\]
Now, taking the root both sides
$ \Rightarrow x = \sqrt {48} = 4\sqrt 3 $
Here, we have used only the positive value because the side of a triangle can never be negative.
Now, the perimeter of the equilateral triangle $ = 3a = 3 \times 4\sqrt 3 = 12\sqrt 3 $.

Therefore, the perimeter of the equilateral triangle is $12\sqrt 3 $.

Note: We know that the perimeter of a polygon is the sum of all sides. Here it is given that the triangle is an equilateral triangle. Therefore, we have used the formula to find its perimeter. If it was not equilateral then we have to add all the sides individually to find its perimeter.