Question

The Qutab Minar casts a shadow 150m long at the same time when the Vikas Minar casts a shadow of 120m long on the ground. If the height of Vikas Minar is 80m, find the height of Qutub Minar.
A. 180m
B. 100m
C. 150m
D. 120m

Answer 1

Hint: The shadow of Qutab Minar and Vikas Minar cast at the same time so the leaning angle of both shadows will be the same. So we can use the formulae \[\tan \alpha =\dfrac{height}{base}\] to find the leaning angle. Put the value in the question and evaluate it to find the value. After finding the leaning angel we can use it to find the height of Qutub Minar by calculating the rest of the problem.

Complete step-by-step answer:
According to the question the height of shadow of Qutab Minar is 150m when the height of the shadow of Vikash Minar is 120m.
We can understand from this that the height of the sun is the same when both the shadows are measured. So that the leaning angel of the shadow is also the same.
Let the leaning angle be \[\alpha \].

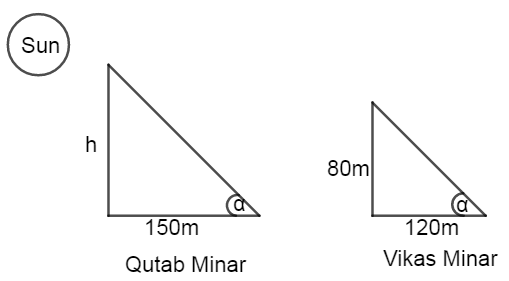
Here in the diagram we can clearly see that the leaning angle of the shadow is \[\alpha \].
The height of Vikas Minar is 80m.
We know the base and height and leaning angle of a triangle. Hence we can use the formulae \[\tan \alpha =\dfrac{height}{base}\]. By putting the value of base=120m and height=80m we can find the leaning angle of the shadow of the Vikas Miner.
\[\begin{align}
  & \tan \alpha =\dfrac{80}{120} \\
 & \Rightarrow \tan \alpha =\dfrac{8}{12} \\
 & \Rightarrow \tan \alpha =\dfrac{2}{3} \\
\end{align}\]

So the leaning angle of the shadow is \[\tan \alpha =\dfrac{2}{3}\].
According to the question the Qutub Minar casts a shadow at the same time when the Vikas Minar casts a shadow. So the leaning angle of the shadow of Qutub Minar and Vikash Minar is the same.
Let us assume the height of Qutub Minar is h.
Now,
\[\tan \alpha =\dfrac{h}{150}\]
Putting the value of \[\tan \alpha \] we get,
\[\Rightarrow \dfrac{2}{3}=\dfrac{h}{150}\]
Cross-multiplying both side,
\[\Rightarrow 3h=300\]
\[\Rightarrow h=\dfrac{300}{3}\]
\[\Rightarrow h=100\]

The height of Qutub Minar is 100m (Option B).

Note: Students have to understand the leaning angle of the shadow. They might take the right angle \[\left( {{90}^{\circ }} \right)\] as a leaning angle and then the calculation would go horribly wrong. Students have to remember the value of \[\tan \alpha \] which is \[\tan \alpha =\dfrac{height}{base}\] . If they write it as \[\tan \alpha =\dfrac{base}{height}\] they will get this math problem wrong.