Question

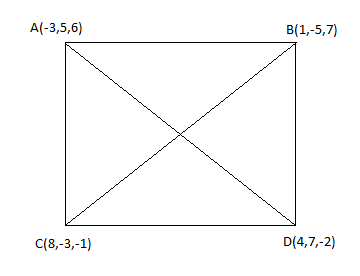
The quadrangle with the vertices \[A\left( { - 3,5,6} \right)\], \[B\left( {1, - 5,7} \right)\], \[C\left( {8, - 3, - 1} \right)\], and \[D\left( {4,7, - 2} \right)\] is a
(a) Square
 (b) Rectangle
 (c) Parallelogram
 (d) Trapezoid

Answer 1

Hint: Here, we need to find the type of the given quadrangle. We will use the distance formula to find the lengths of the four sides of the quadrangle. Then, we will again use the distance formula to find the lengths of the diagonals of the quadrangle. Using the length of diagonals and sides, we can determine which type of quadrangle is the correct answer.

Formula Used: The distance between two points \[\left( {{x_1},{y_1},{z_1}} \right)\] and \[\left( {{x_2},{y_2},{z_2}} \right)\] is given by the formula \[\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} \].

Complete step-by-step answer:
We will find the lengths of the four sides of the quadrangle using the distance formula.

Substituting \[{x_1} = - 3\], \[{y_1} = 5\], \[{z_1} = 6\], \[{x_2} = 1\], \[{y_2} = - 5\], and \[{z_2} = 7\] in the distance formula \[\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} \], we get
\[ \Rightarrow AB = \sqrt {{{\left[ {1 - \left( { - 3} \right)} \right]}^2} + {{\left( { - 5 - 5} \right)}^2} + {{\left( {7 - 6} \right)}^2}} \]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow AB = \sqrt {{{\left( {1 + 3} \right)}^2} + {{\left( { - 5 - 5} \right)}^2} + {{\left( {7 - 6} \right)}^2}} \\ \Rightarrow AB = \sqrt {{4^2} + {{\left( { - 10} \right)}^2} + {1^2}} \end{array}\]
Applying the exponents on the bases, we get
\[ \Rightarrow AB = \sqrt {16 + 100 + 1} \]
Adding the terms of the expression, we get
\[ \Rightarrow AB = \sqrt {117} \]
Substituting \[{x_1} = 1\], \[{y_1} = - 5\], \[{z_1} = 7\], \[{x_2} = 8\], \[{y_2} = - 3\], and \[{z_2} = - 1\] in the distance formula, we get
\[ \Rightarrow BC = \sqrt {{{\left( {8 - 1} \right)}^2} + {{\left[ { - 3 - \left( { - 5} \right)} \right]}^2} + {{\left( { - 1 - 7} \right)}^2}} \]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow BC = \sqrt {{{\left( {8 - 1} \right)}^2} + {{\left[ { - 3 + 5} \right]}^2} + {{\left( { - 1 - 7} \right)}^2}} \\ \Rightarrow BC = \sqrt {{7^2} + {2^2} + {{\left( { - 8} \right)}^2}} \end{array}\]
Applying the exponents on the bases, we get
\[ \Rightarrow BC = \sqrt {49 + 4 + 64} \]
Adding the terms of the expression, we get
\[ \Rightarrow BC = \sqrt {117} \]
Substituting \[{x_1} = 8\], \[{y_1} = - 3\], \[{z_1} = - 1\], \[{x_2} = 4\], \[{y_2} = 7\], and \[{z_2} = - 2\] in the distance formula, we get
\[ \Rightarrow CD = \sqrt {{{\left( {4 - 8} \right)}^2} + {{\left[ {7 - \left( { - 3} \right)} \right]}^2} + {{\left[ { - 2 - \left( { - 1} \right)} \right]}^2}} \]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow CD = \sqrt {{{\left( {4 - 8} \right)}^2} + {{\left( {7 + 3} \right)}^2} + {{\left( { - 2 + 1} \right)}^2}} \\ \Rightarrow CD = \sqrt {{{\left( { - 4} \right)}^2} + {{10}^2} + {{\left( { - 1} \right)}^2}} \end{array}\]
Applying the exponents on the bases, we get
\[ \Rightarrow CD = \sqrt {16 + 100 + 1} \]
Adding the terms of the expression, we get
\[ \Rightarrow CD = \sqrt {117} \]
Substituting \[{x_1} = 4\], \[{y_1} = 7\], \[{z_1} = - 2\], \[{x_2} = - 3\], \[{y_2} = 5\], and \[{z_2} = 6\] in the distance formula, we get
\[ \Rightarrow DA = \sqrt {{{\left( { - 3 - 4} \right)}^2} + {{\left( {5 - 7} \right)}^2} + {{\left[ {6 - \left( { - 2} \right)} \right]}^2}} \]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow DA = \sqrt {{{\left( { - 3 - 4} \right)}^2} + {{\left( {5 - 7} \right)}^2} + {{\left( {6 + 2} \right)}^2}} \\ \Rightarrow DA = \sqrt {{{\left( { - 7} \right)}^2} + {{\left( { - 2} \right)}^2} + {8^2}} \end{array}\]
Applying the exponents on the bases, we get
\[ \Rightarrow DA = \sqrt {49 + 4 + 64} \]
Adding the terms of the expression, we get
\[ \Rightarrow DA = \sqrt {117} \]
We can observe that all the four sides are equal to \[\sqrt {117} \].
Now, we will find the lengths of the diagonals of the quadrangle.
Substituting \[{x_1} = 8\], \[{y_1} = - 3\], \[{z_1} = - 1\], \[{x_2} = - 3\], \[{y_2} = 5\], and \[{z_2} = 6\] in the distance formula, we get
\[ \Rightarrow AC = \sqrt {{{\left( { - 3 - 8} \right)}^2} + {{\left[ {5 - \left( { - 3} \right)} \right]}^2} + {{\left[ {6 - \left( { - 1} \right)} \right]}^2}} \]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow AC = \sqrt {{{\left( { - 3 - 8} \right)}^2} + {{\left( {5 + 3} \right)}^2} + {{\left( {6 + 1} \right)}^2}} \\ \Rightarrow AC = \sqrt {{{\left( { - 11} \right)}^2} + {8^2} + {7^2}} \end{array}\]
Applying the exponents on the bases, we get
\[ \Rightarrow AC = \sqrt {121 + 64 + 49} \]
Adding the terms of the expression, we get
\[ \Rightarrow AC = \sqrt {234} \]
Substituting \[{x_1} = 4\], \[{y_1} = 7\], \[{z_1} = - 2\], \[{x_2} = 1\], \[{y_2} = - 5\], and \[{z_2} = 7\] in the distance formula, we get
\[ \Rightarrow BD = \sqrt {{{\left( {1 - 4} \right)}^2} + {{\left( { - 5 - 7} \right)}^2} + {{\left[ {7 - \left( { - 2} \right)} \right]}^2}} \]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow BD = \sqrt {{{\left( {1 - 4} \right)}^2} + {{\left( { - 5 - 7} \right)}^2} + {{\left( {7 + 2} \right)}^2}} \\ \Rightarrow BD = \sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 12} \right)}^2} + {9^2}} \end{array}\]
Applying the exponents on the bases, we get
\[ \Rightarrow BD = \sqrt {9 + 144 + 81} \]
Adding the terms of the expression, we get
\[ \Rightarrow BD = \sqrt {234} \]
Therefore, we can observe that the diagonals are equal to \[\sqrt {234} \].
Since the four sides of the quadrangle are equal to each other, and the diagonals are also equal to each other, the quadrangle with the vertices \[A\left( { - 3,5,6} \right)\], \[B\left( {1, - 5,7} \right)\], \[C\left( {8, - 3, - 1} \right)\], and \[D\left( {4,7, - 2} \right)\] is a square.
Thus, the correct option is option (a).

Note: We need to check the lengths of the diagonals of the quadrangle also. This is because if all the four sides are equal but the diagonals are not equal, then the given quadrangle would be a rhombus, and not a square. Therefore, we cannot say that since all the four sides are equal, the quadrangle is a square. If the opposite sides of a quadrangle are equal then it is called a rectangle. In parallelogram, the opposite sides are parallel. So, to solve the question we need to know about different quadrangles.