Question

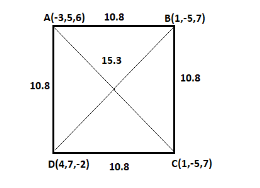
The quadrangle with the vertices \[A( - 3,5,6),B(1, - 5,7),C(8, - 3, - 1)\] and \[D(4,7, - 2)\] is a
A.Square
B.Rectangle
C.Parallelogram
D.Trapezoid

Answer 1

Hint: In this problem, we need to solve the quadrangle with the vertices to find the solution frame a shape with the length of the quadrangle. In geometrical representation, flat shape that has four sides and four angles: an open square or rectangular area that is surrounded by buildings on all four sides. Square is a quadrilateral with four equal sides and angles. It's also a regular quadrilateral as both its sides and angles are equal.

Complete step by step solution:
In the given problem,
Vertices of the quadrangle are \[A( - 3,5,6),B(1, - 5,7),C(8, - 3, - 1)\] and \[D(4,7, - 2)\]
We need to find the length of the sides of the quadrangle, we get
The length of the quadrangle formula is \[\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \]
To find the length of the quadrangle \[AB,BC,CD\] and \[AD\] , we get
For finding the length, \[AB\] from the vertices are \[A( - 3,5,6),B(1, - 5,7)\]
 \[AB = \sqrt {{{(1 - ( - 3))}^2} + {{( - 5 - 5)}^2} + {{(7 - 6)}^2}} = \sqrt {{{(4)}^2} + {{( - 10)}^2} + {{(1)}^2}} \]
By simplify the sum of the square, we get
 \[AB = \sqrt {16 + 100 + 1} \]
By performing the addition, we get
 \[AB = \sqrt {117} = 10.82\]
Therefore, the length of \[AB\] is \[10.82\]
For finding the length, \[BC\] from the vertices are \[B(1, - 5,7),C(8, - 3, - 1)\]
 \[BC = \sqrt {{{(8 - 1)}^2} + {{( - 3 - ( - 5))}^2} + {{( - 1 - 7)}^2}} = \sqrt {{{(7)}^2} + {{(2)}^2} + {{( - 8)}^2}} \]
By simplify the sum of the square, we get
 \[BC = \sqrt {49 + 4 + 64} \]
By performing the addition, we get
 \[BC = \sqrt {117} = 10.82\]
Therefore, the length of \[BC\] is \[10.82\]
For finding the length, \[CD\] from the vertices are \[C(8, - 3, - 1),D(4,7, - 2)\]
 \[CD = \sqrt {{{(4 - 8)}^2} + {{(7 - ( - 3))}^2} + {{( - 2 - ( - 1))}^2}} = \sqrt {{{( - 4)}^2} + {{(10)}^2} + {{( - 1)}^2}} \]
By simplify the sum of the square, we get
 \[CD = \sqrt {16 + 100 + 1} \]
By performing the addition, we get
 \[CD = \sqrt {117} = 10.82\]
Therefore, the length of \[CD\] is \[10.82\]
For finding the length, \[AD\] from the vertices are \[A( - 3,5,6),D(4,7, - 2)\]
 \[AD = \sqrt {{{(4 - ( - 3))}^2} + {{(7 - 5)}^2} + {{( - 2 - 6)}^2}} = \sqrt {{{(7)}^2} + {{(2)}^2} + {{( - 8)}^2}} \]
By simplify the sum of the square, we get
 \[AD = \sqrt {49 + 4 + 64} \]
By performing the addition, we get
 \[AD = \sqrt {117} = 10.82\]
Therefore, the length of \[AD\] is \[10.82\]
Since, the length of the four sides are equal.
Then, we needs to finding the length of diagonals, we get
For the length, \[AC\] vertices are \[A( - 3,5,6),C(8, - 3, - 1)\]
 \[AC = \sqrt {{{(8 - ( - 3))}^2} + {{( - 3 - 5)}^2} + {{( - 1 - 6)}^2}} = \sqrt {{{(11)}^2} + {{( - 8)}^2} + {{( - 7)}^2}} \]
By simplify the sum of the square, we get
 \[AC = \sqrt {121 + 64 + 49} \]
By performing the addition, we get
 \[AC = \sqrt {234} = 15.3\]
Therefore, the length of \[AC\] is \[15.3\]
For the length, \[BD\] vertices are \[B(1, - 5,7),D(4,7, - 2)\]
 \[BD = \sqrt {{{(4 - 1)}^2} + {{(7 - ( - 5))}^2} + {{( - 2 - 7)}^2}} = \sqrt {{{(3)}^2} + {{(12)}^2} + {{( - 9)}^2}} \]
By simplify the sum of the square, we get
 \[BD = \sqrt {9 + 144 + 81} \]
By performing the addition, we get
 \[BD = \sqrt {234} = 15.3\]
Therefore, the length of \[BD\] is \[15.3\]
Since, the length of two diagonals are equal.
Hence, the quadrangle formed by the vertices \[A,B,C\] and \[D\] is a square.

The final answer is option (A) Square
So, the correct answer is “Option A”.

Note: We note the quadrangle frame the square shape with the length of the quadrangle. Square is a quadrilateral with four equal sides and angles. It's also a regular quadrilateral as both its sides and angles are equal. It can be found by the length of quadrangle formula you have remember is \[\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \] . Flat shape that has four sides and four angles: an open square or rectangular area that is surrounded by buildings on all four sides.