Question

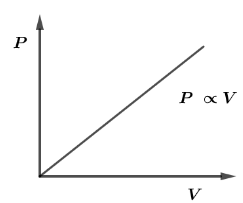
The PV Diagram of an ideal monatomic gas is shown in the figure given below. The molar heat capacity of the gas will be

A. $2R$
B. $3R$
C. $5R$
D. $7R$

Answer 1

Hint: In thermodynamics, a monatomic gas is one in which atoms of the gas are not bound to each other such that gas consist of multiple single atoms of particular type and when such type of monoatomic gases behave ideally such that gas obeys the ideal gas equation perfectly which is $PV = nRT$ is called ideal monatomic gas. Here, we will examine the relation between P and V from the given graph and will derive the value of molar heat capacity.

Complete step by step answer:
We should know that molar heat capacity is known as the amount of energy needed for a gas of $1\,mole$ in order to increase the temperature of the gas by one unit.Mathematically, molar heat capacity is calculated as
$C = {C_V} - \dfrac{R}{{n - 1}}$
where, ${C_V}$ is the heat capacity of monatomic gas at constant volume which has a fixed value of ${C_V} = \dfrac{{3R}}{2}$, $R$ Is the universal gas constant and $n$ is the value from relation pressure-Volume of a gas is related as $P{V^n}$.

Now, from the given graph, pressure versus Volume we have a straight line which means pressure is directly proportional to the volume and mathematically, it can be written as
$P \propto V$
$\Rightarrow P{V^{ - 1}} = $ Constant
So comparing $P{V^{ - 1}}$ with $P{V^n}$ us get,
$n = - 1$
Now, from using the formula of molar heat capacity we have $C = {C_V} - \dfrac{R}{{n - 1}}$ , put
${C_V} = \dfrac{{3R}}{2}$
$\Rightarrow n = - 1$
We get,
$C = \dfrac{{3R}}{2} + \dfrac{R}{2}$
$\therefore C = 2R$
So, the molar heat capacity of the gas is $C = 2R$

Hence, the correct option is A.

Note: It should be remembered that, Heat capacity of the gas when measured with constant volume for a monatomic gas is denoted by ${C_V} = \dfrac{{3R}}{2}$ and when heat capacity measured with constant pressure its denoted by ${C_P} = \dfrac{{5R}}{2}$ which has a fixed value. The universal gas constant has a fixed numerical value which is $8.314Jmo{l^{ - 1}}{K^{ - 1}}$.