Question

The pulleys in figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.

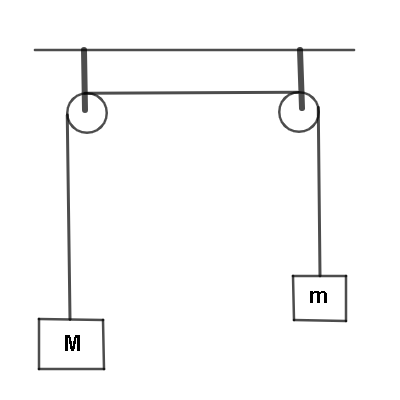
Answer 1

Hint: We will first label all the diagrams mentioning the tensions in strings , accelerations and weights. Then we will form certain equations that will include all the forces due to the pulley, and the blocks to finally get the value of acceleration of block M.

Complete answer:

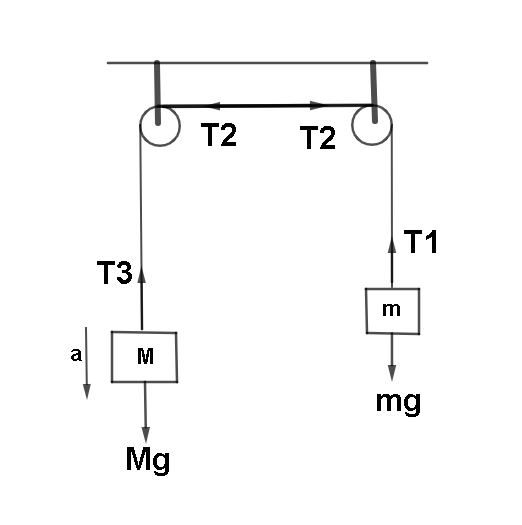
Here T stands for tension in strings and a stands for acceleration.
Now let's form equations : considering the mass M, we get:
\[Mg - {T_1} = Ma\;\;\;...(1)\]
Also,
\[({T_1} - {T_2})R = I\dfrac{\alpha }{R}\] (where \[\alpha \] is angular acceleration)
Or,
\[ \Rightarrow ({T_1} - {T_2}) = I\dfrac{\alpha }{{{R^2}}}\;\;...(2)\]
Similarly,
\[ \Rightarrow ({T_2} - {T_3})R = I\dfrac{\alpha }{{{R^2}}}\;\;...(3)\]
And
\[ \Rightarrow {T_3} - mg = ma\;\;\;\;\;\;\;\;\;...(4)\]
Looking at the above equations we will now add equations 2 and 3.
We will get as follows:
\[({T_1} - {T_3}) = \dfrac{{2I\alpha }}{{{R^2}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;.......(5)\]
Again by adding equations 1 and 4 we will get as follows:
\[ - mg + Mg + ({T_3} - {T_1}) = Ma + ma.......(6)\]
We will now substitute the value of \[{T_3} - {T_1}\] from equation 5 in equation 6.
We will get;
\[ \Rightarrow Mg - mg = Ma + ma + \dfrac{{2I\alpha }}{{{R^2}}}\]
From this we will get the acceleration of block M as,
\[ \Rightarrow a = \dfrac{{(M - m)G}}{{(M + m + \dfrac{{2I}}{{{R^2}}})}}\].

Additional information:
A pulley is a wheel on an axle or shaft that allows a taut cable or belt to move and change directions while also transferring power between the shaft and the cable or belt..

Note:
Remember according to equation 5, \[({T_1} - {T_3})\;\] has been found but we need \[{T_3} - {T_1}\]. Hence do not forget to change the sign .
Be very careful while assigning the directions of tensions in the strings. Short trick to remember is that tension will be away from mass.