Question

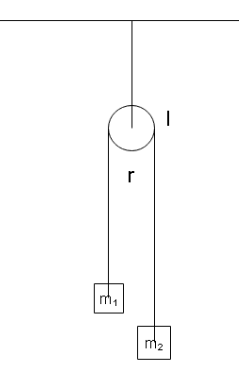
The pulley shown in the figure has a moment of inertia $ I $ about its axis and its radius is $ r $ . Calculate the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.

Answer 1

Hint: Assume that mass $ {m_2} $ is greater than $ {m_1} $ so $ {m_2} $ will fall on one side and $ {m_1} $ will rise on one side. The acceleration of the blocks can be calculated by balancing the linear acceleration associated with the angular motion of the rod with the accelerations of the blocks.

Formula used:
 $ a = \alpha \times r $ where $ a $ is the linear acceleration associated with a rotated body of angular acceleration $ \alpha $ and linear displacement $ r $

Complete step by step solution:
We’ve been given that the string that connects the two blocks does not slip on the pulley. So whenever one mass falls and the other rises, the string moves the pulley along with it. Let us consider the linear acceleration due to the difference in mass of the blocks.
Since the string is under force, it will have tension in it. For the block of mass $ {m_1} $ that rises upwards with a net acceleration $ a $ , we can write the equation of motion as
 $ {m_1}g - {T_1} = {m_1}a $
Similarly we can write the equation of the mass $ {m_2} $ that is moving downwards with a net acceleration $ a $ as:
 $ {T_2} - {m_2}g = {m_2}a $
Now, the pulley will have the same angular acceleration as the string on it since the string does not slip on the pulley. The angular acceleration on the string can be equalized with the angular acceleration of the pulley as
 $ {T_1}r - {T_2}r = I\alpha $
Since $ a = \alpha \times r $ , we can write
 $ {T_1}r - {T_2}r = \dfrac{{Ia}}{r} $
Substituting the values of $ {T_1} $ and $ {T_2} $ from equation (1) and (2), we get
 $ [({m_1}g - a) - {m_2}(g + a)]r = \dfrac{{Ia}}{r} $
Solving for $ a\; $ we can write
 $ a = \dfrac{{({m_1} - {m_2})g{r^3}}}{{I + ({m_1} + {m_2}){r^2}}} $ .

Note:
The tricky part in this question is realizing that the angular motion of the pulley is due to the motion of the string on it without slipping. In a real-world scenario, there is always some slippage of the string on the pulley as well as other friction forces that act between the string and the pulley.