Question

The P-T and V-T diagrams of an isochoric process of $n$ moles of an ideal gas from pressure ${P_0}$​, volume ${V_0}$​ to pressure $4{P_0}$​, indicating the pressures and temperatures of the gas in the initial and the final states will be __________.

Answer 1

Hint : In an isochoric process, the volume of the system remains constant while the system undergoes the process. Using the ideal gas law we can relate the pressure, volume, and temperature of an ideal gas in the initial and the final states of the gas.

Formula used: In this question, we will use the following formula:
$PV = nRT$where $P$ is the pressure of the gas, $V$ is the volume, $n$ is the number of moles, $R$ is the gas constant, and $T$ is the temperature of the gas

Complete step by step answer
We’ve been given an isochoric process of $n$ moles of an ideal gas from pressure ${P_0}$​, volume ${V_0}$​ to pressure $4{P_0}$​. Since the process is isochoric, the volume of the process remains constant and we can say that the volume of the gas in the final state will also be ${V_0}$.
Using the ideal gas law, we can write
$PV = nRT$
$ \Rightarrow V = \dfrac{{nRT}}{P}$
Since the volume of the gas remains constant, we can write
$\dfrac{{{T_1}}}{{{P_1}}} = \dfrac{{{T_2}}}{{{P_2}}}$
$\dfrac{{{T_1}}}{{{P_0}}} = \dfrac{{{T_2}}}{{4{P_0}}}$
Cross multiplying the numerator and denominator, we get
$4{T_1} = {T_2}$
We can now form the P-T and V-T diagrams knowing the initial and final stage of the gas as shown below

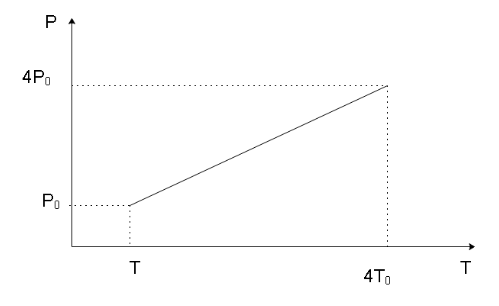
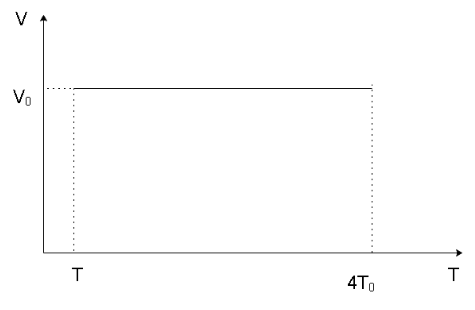
Note
Since the process is isochoric, we can get a hint that in the P-V graph, the line indicating the process will be parallel to the $y$ -axis. Similarly, in the V-T graph, the line indicating the process will be parallel to the $x$ -axis which can also be stated as the process line will be in a direction perpendicular to the direction of the volume axis as the volume of the system remains constant in the process and will have a singular value.