Question

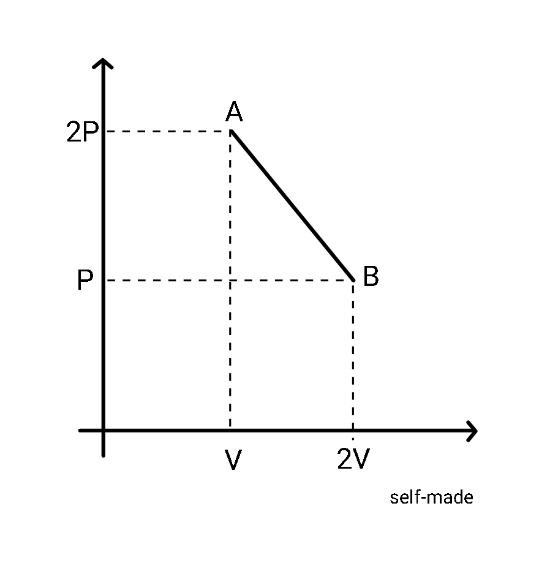
The process AB is shown in the diagram. As the gas is taken from A to B, its temperature
(A) initially increases then decreases.
(B) initially decreases then decreases.
(C) remains constant.
(D) variation depends on the type of gas.

Answer 1

Hint : Here, you are given a pressure versus volume graph in which the gas is taken from state A where the pressure is $ 2P $ and the volume is $ V $ to state B where the pressure is $ P $ and the volume is $ 2V $ . You are asked to find the variation in temperature as the gas is taken from state A to state B, you have to conclude whether the temperature increases or decreases or remains constant or you can see the options for the various possibilities. In order to answer this question, you need to consider the ideal gas equation and use it to find the variation of temperature with any of the above-mentioned quantities, that is pressure or volume.

Complete Step By Step Answer:
Here, in the graph we are given variation of pressure as the volume changes. It can be seen that the equation of dependence of pressure on volume is a straight line. Let us write the equation of the line. We have two points on the graph, point A and point B, pressure and volume at each point is known to us, so we can write the equation of line as,
 $
  \dfrac{{p - 2P}}{{2P - P}} = \dfrac{{v - V}}{{V - 2V}} \\
  \dfrac{{p - 2P}}{P} = \dfrac{{v - V}}{{ - V}} \\
  p - 2P = - \dfrac{P}{V}v + P \\
  p = - \dfrac{P}{V}v + 3P \\
  $
Here, $ p $ and $ v $ are arbitrary pressure and volume.
As you know that the ideal gas equation is $ pv = nRT $ or $ pv = cT $ , we get pressure from here as $ p = \dfrac{{cT}}{v} $ . Let us substitute this in the equation of line.
 $
  p = - \dfrac{P}{V}v + 3P \\
  \dfrac{{cT}}{v} = - \dfrac{P}{V}v + 3P \\
  cT = - \dfrac{P}{V}{v^2} + 3Pv \\
  $
Now, let us differentiate temperature with respect to volume and equate it to zero.
 $
  c\dfrac{{dT}}{{dv}} = - \dfrac{{2P}}{V}v + 3P \\
  c\dfrac{{dT}}{{dv}} = 0 \\
   - \dfrac{{2P}}{V}v + 3P = 0 \\
  v = \dfrac{{3V}}{2} \\
  $
The derivative is zero at $ v = \dfrac{{3V}}{2} $ which is between $ V $ and $ 2V $ , which means that it is either a minima or a maxima. Now, let us find the second derivative.
 $ c\dfrac{{{d^2}T}}{{d{v^2}}} = - \dfrac{{2P}}{V} < 0 $ , always negative. This means that $ v = \dfrac{{3V}}{2} $ is a maxima which means that the temperature first increases and then decreases.
Therefore, as the gas is taken from A to B, its temperature initially increases then decreases.
Option (A) is correct.

Note :
Here, you were given a graph of pressure versus volume and were asked to comment on temperature, so we used the help of the ideal gas equation to solve our problem, so keep this trick in mind. Also, remember the maxima and minima trick we used here to determine the variation of temperature with respect to volume.