Question

The principal amplitude of \[\left( 2-i \right){{\left( 1-2i \right)}^{2}}\] is in the interval
(A) \[\left( 0,\dfrac{\pi }{2} \right)\]
(B) \[\left( -\dfrac{\pi }{2},0 \right)\]
(C) \[\left( -\pi ,-\dfrac{\pi }{2} \right)\]
(D) \[\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)\]

Answer 1

Hint: First of all, expand the given expression \[\left( 2-i \right){{\left( 1-2i \right)}^{2}}\] using the formula \[{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\] . We know that, \[{{i}^{2}}=-1\] . Now, replace \[{{i}^{2}}\] by -1 and then simplify the expression. Then, draw the diagram for the axis of real and imaginary part of the complex number. We can see that the complex number \[\left( 2-i \right){{\left( 1-2i \right)}^{2}}\] lies in the third quadrant. We know that the principle amplitude varies from \[-\pi \] to \[\pi \] . Now, conclude the principal amplitude.

Complete step-by-step answer:
According to the question, we have the expression,
\[\left( 2-i \right){{\left( 1-2i \right)}^{2}}\] ……………………………(1)
We can see that the expression has the term \[i\] and \[i\] is imaginary. It means that the given expression is complex.
We know the formula, \[{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\] ………………………….(2)
Replacing a by 1 and b by \[2i\] in equation (2), we get
\[{{\left( 1-2i \right)}^{2}}={{1}^{2}}+{{\left( 2i \right)}^{2}}-2.1.2i\] …………………………(3)
First of all, expand the given expression.
From equation (1) and equation (3), we get
\[\begin{align}
  & \left( 2-i \right){{\left( 1-2i \right)}^{2}} \\
 & =\left( 2-i \right)\left( {{1}^{2}}+{{\left( 2i \right)}^{2}}-2.1.2i \right) \\
\end{align}\]
\[=\left( 2-i \right)\left( 1+4{{i}^{2}}-4i \right)\] …………………………….(4)
We know that, \[{{i}^{2}}=-1\] ………………….(5)
Now, from equation (4) and equation (5), we get
\[\begin{align}
  & =\left( 2-i \right)\left( 1+4\left( -1 \right)-4i \right) \\
 & =\left( 2-i \right)\left( 1-4-4i \right) \\
\end{align}\]
\[=\left( 2-i \right)\left( -3-4i \right)\] ………………………….(6)
Now, further expanding equation (6), we get
\[\begin{align}
  & =\left( 2-i \right)\left( -3-4i \right) \\
 & =\left( -6-8i+3i+4{{i}^{2}} \right) \\
\end{align}\]
\[=\left( -6-5i+4{{i}^{2}} \right)\] ………………………(7)
From equation (5) and equation (7), we get
\[\begin{align}
  & =\left( -6-5i+4\left( -1 \right) \right) \\
 & =\left( -6-5i-4 \right) \\
\end{align}\]
\[=\left( -10-5i \right)\] ……………………..(8)
We also know the plane of the complex number. In the plane, the horizontal axis represents the real part of the complex number while the vertical axis represents the imaginary part of the complex number.
Let us draw the diagram for the axis of real and imaginary part of the complex number.

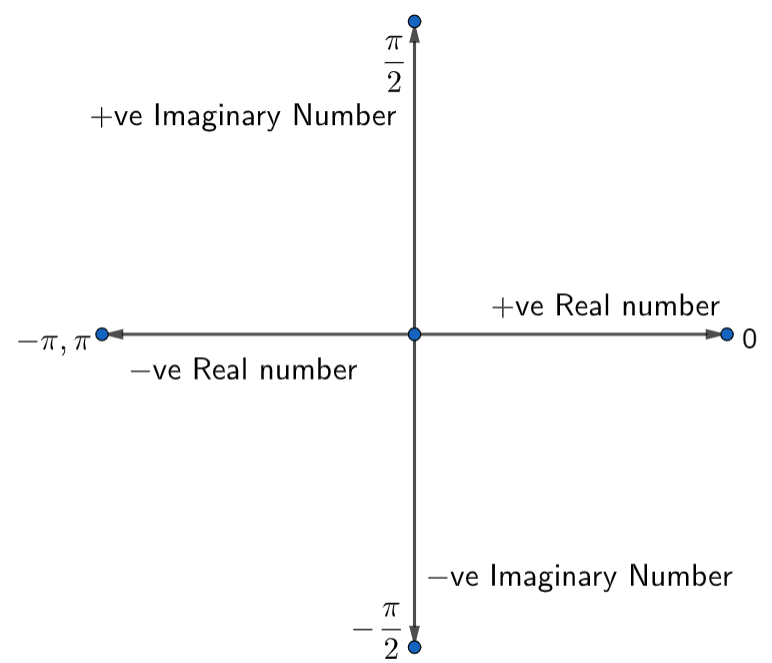
In the complex number \[\left( -10-5i \right)\] , the real part is -10 and the imaginary part is \[-5i\] .
Here, both the real part and imaginary part are negative. And from the diagram, we can figure it out that both parts can be negative only in the third quadrant.
So, the complex number \[\left( -10-5i \right)\] lies in the third quadrant.
We know that the principle amplitude varies from \[-\pi \] to \[\pi \] .
Our complex number \[\left( -10-5i \right)\] in the third quadrant.
So, we have to move from \[-\pi \] to \[\dfrac{-\pi }{2}\] .
Therefore, the principal amplitude of the complex number \[\left( 2-i \right){{\left( 1-2i \right)}^{2}}\] lies in the interval \[-\pi \] to \[\dfrac{-\pi }{2}\] .
Hence, the correct option is (C).

Note: Since the complex number \[\left( 2-i \right){{\left( 1-2i \right)}^{2}}\] lies in the third quadrant so, might take the principal amplitude as \[\left( \pi ,\dfrac{3\pi }{2} \right)\] . This is wrong because the principal amplitude of the complex number lies in the range \[\left( -\pi ,\pi \right)\] . The principal amplitude \[\left( \pi ,\dfrac{3\pi }{2} \right)\] does not lie in the range \[\left( -\pi ,\pi \right)\] . Therefore, we have only those intervals of principal amplitude which lie in the range \[\left( -\pi ,\pi \right)\] . Hence, the principal amplitude of the complex number \[\left( 2-i \right){{\left( 1-2i \right)}^{2}}\] lies in the interval \[-\pi \] to \[\dfrac{-\pi }{2}\] .